题目内容
设数列{an}的前n项和为Sn,已知a1=1,Sn=nan-n(n-1)(n=1,2,3…).数列{bn}满足bn=
,Tn为数列bn的前n项和.
(1)求an和Tn;
(2)若对于任意的n∈N+,不等式λTn<n+8(-1)n恒成立,求实数λ的取值范围.
| 1 |
| anan+1 |
(1)求an和Tn;
(2)若对于任意的n∈N+,不等式λTn<n+8(-1)n恒成立,求实数λ的取值范围.
考点:数列与不等式的综合
专题:计算题,等差数列与等比数列,不等式的解法及应用
分析:(1)当n≥2时,an=Sn-Sn-1=nan-(n-1)an-1-2(n-1),易证an-an-1=2(n≥2,n∈N*),于是可得:{an}是等差数列,再由等差数列的通项公式,即可得到通项,再由裂项相消求和,求得Tn;
(2)分别讨论n为奇数和偶数,运用分离参数,讨论右边的最小值,注意运用单调性和基本不等式,即可得到范围.
(2)分别讨论n为奇数和偶数,运用分离参数,讨论右边的最小值,注意运用单调性和基本不等式,即可得到范围.
解答:
解:(1)当n≥2,n∈N*时,由已知Sn=nan-n(n-1)
得Sn-1=(n-1)an-1-(n-1)(n-2).
两式相减得Sn-Sn-1=nan-(n-1)an-1-2(n-1).
又Sn-Sn-1=an,所以(n-1)an-(n-1)an-1=2(n-1).
即an-an-1=2(n≥2,n∈N*).
所以{an}是以1为首项、2为公差的等差数列,
即an=1+2(n-1)=2n-1,
bn=
=
=
(
-
).
则Tn=b1+b2+…+bn=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
).
则Tn=
;
(2)由于对任意的n∈N+,不等式λTn<n+8(-1)n恒成立,
则当n为奇数时,有λTn<n-8恒成立,
即有λ<
=2n-
-15,
由于2n-
-15在n≥1上递增,则n=1取得最小值,且为-21,
则λ<-21;
当n为偶数时,有λTn<n+8恒成立,
即有λ<
=2n+
+17,
由于2n+
+17≥2
+17=25,当且仅当n=2,取得最小值,且为25.
则λ<25.
由于对任意的n∈N+,不等式恒成立,则λ<-21.
则实数λ的取值范围是(-∞,-21).
得Sn-1=(n-1)an-1-(n-1)(n-2).
两式相减得Sn-Sn-1=nan-(n-1)an-1-2(n-1).
又Sn-Sn-1=an,所以(n-1)an-(n-1)an-1=2(n-1).
即an-an-1=2(n≥2,n∈N*).
所以{an}是以1为首项、2为公差的等差数列,
即an=1+2(n-1)=2n-1,
bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则Tn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
则Tn=
| n |
| 2n+1 |
(2)由于对任意的n∈N+,不等式λTn<n+8(-1)n恒成立,
则当n为奇数时,有λTn<n-8恒成立,
即有λ<
| (n-8)(2n+1) |
| n |
| 8 |
| n |
由于2n-
| 8 |
| n |
则λ<-21;
当n为偶数时,有λTn<n+8恒成立,
即有λ<
| (n+8)(2n+1) |
| n |
| 8 |
| n |
由于2n+
| 8 |
| n |
2n•
|
则λ<25.
由于对任意的n∈N+,不等式恒成立,则λ<-21.
则实数λ的取值范围是(-∞,-21).
点评:本题考查数列的通项和求和,着重考查运算、推理的能力,突出考查等差关系的确定与裂项法求和的综合应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|x>2},B={x|1<x<3},则(∁RA)∩B=( )
| A、{x|x>2} |
| B、{x|x>1} |
| C、{x|2<x<3} |
| D、{x|1<x≤2} |
直线y=kx-2交抛物线y2=8x于A、B两点,若弦AB的中点M(2,m),则k=( )
| A、2或-1 | B、-1 | C、2 | D、3 |
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,若在右支上存在点A,使得点F2到直线AF1的距离为2a,则该双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,+∞) |
在△ABC中,已知角A=60°,边b=1,三角形的面积为
,则边c=( )
| 3 |
| A、5 | ||
B、
| ||
| C、4 | ||
| D、3 |
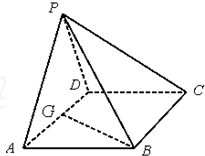 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.