题目内容
已知函数f(x)=
sin2x+2cos2x-3
(Ⅰ)求f(
)的值
(Ⅱ)求f(x)在[-
,
]的最大值和最小值.
| 3 |
(Ⅰ)求f(
| π |
| 3 |
(Ⅱ)求f(x)在[-
| π |
| 6 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值
分析:(1)化简可得f(x)=2sin(2x+
)-2,代值计算可得;
(2)由(1)知f(x)=2sin(2x+
)-2,由x∈[-
,
]结合三角函数的值域可得.
| π |
| 6 |
(2)由(1)知f(x)=2sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 4 |
解答:
解:(1)化简可得f(x)=
sin2x+2cos2x-3
=
sin2x+cos2x-2=2sin(2x+
)-2,
代值计算可得f(
)=2sin(
+
)-2=-1
(2)由(1)知f(x)=2sin(2x+
)-2,
∵x∈[-
,
],∴2x+
∈[-
,
],
∴sin(
+
)∈[-
,1],
∴f(x)∈[-3,0]
∴f(x)最大值为0,最小值为-3
| 3 |
=
| 3 |
| π |
| 6 |
代值计算可得f(
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
(2)由(1)知f(x)=2sin(2x+
| π |
| 6 |
∵x∈[-
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴sin(
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
∴f(x)∈[-3,0]
∴f(x)最大值为0,最小值为-3
点评:本题考查三角函数恒等变换,涉及三角函数的最值,属基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知正方形AP1P2P3的边长为4,点B,C分别是边P1P2,P2P3的中点,沿AB,BC,CA折叠成一个三棱锥P-ABC(使P1,P2,P3重合于点P),则三棱锥P-ABC的外接球的体积为( )
| A、24π | ||
B、8
| ||
C、4
| ||
| D、4π |
若函数f(x)在R上是单调递减的奇函数,则下列关系式成立的是( )
| A、f(3)<f(4) |
| B、f(3)<-f(-4) |
| C、-f(-3)<f(-4) |
| D、f(-3)>f(-4) |
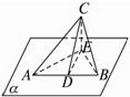 Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.
Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.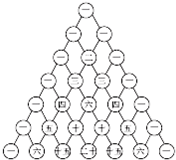 如图中的杨辉三角最早出现于我国南宋数学家杨辉1261年所著的《详解九章算法》.它有很多奇妙的性质,如每个数等于它肩上两数之和.记图中从上到下第i行从左到右第j个数为(i,j).数列{an}的前n项和Sn=(n+2,3),n∈N*.
如图中的杨辉三角最早出现于我国南宋数学家杨辉1261年所著的《详解九章算法》.它有很多奇妙的性质,如每个数等于它肩上两数之和.记图中从上到下第i行从左到右第j个数为(i,j).数列{an}的前n项和Sn=(n+2,3),n∈N*.