题目内容
设F1、F2分别是椭圆(1)求该椭圆的离心率;
(2)若点E到椭圆的右准线的距离为![]() ,过椭圆的上顶点A的直线与⊙F2交于B、C两点,且
,过椭圆的上顶点A的直线与⊙F2交于B、C两点,且![]() =λ
=λ![]() ,求λ的取值范围.
,求λ的取值范围.
解:(1)由题意可知:⊙F2的半径为b,EF1⊥EF2,
∴(2a-b)2+b2=4(a2-b2),
即2a=3b.∴椭圆的离心率为![]() .
.
(2)由椭圆的定义可得:b=![]() ×
×![]() =2,a=3,∴点F2的坐标为(
=2,a=3,∴点F2的坐标为(![]() ,0).
,0).
∴圆的方程为(x-![]() )2+y2=4.
)2+y2=4.
∴点A在圆外,且AB·AC=5.∴λAC2=5.
若λ<1,则5<AC≤5,此时![]() ≤λ<1;
≤λ<1;
若λ>1,则1≤AC<![]() ,此时1<λ≤5.
,此时1<λ≤5.
另解:由椭圆的定义可得:b=![]() ×
×![]() =2,a=3,
=2,a=3,
∴点F2的坐标为(![]() ,0).
,0).
∴圆的方程为(x-![]() )2+y2=4.
)2+y2=4.
设直线AC的方程为y=kx+2,
由此得-45<k<0.11分
设点B(x1,y1),C(x2,y2),∵![]() =λ
=λ![]() ,∴x1=λx2.
,∴x1=λx2.
由 得(k2+1)x2+(4k-25)x+5=0.
得(k2+1)x2+(4k-25)x+5=0.
∴x1·x2=![]() ,x1+x2=
,x1+x2=![]() .
.
∴λ+![]() =
=![]() +
+![]() =
=![]() -2.
-2.
∴2<λ+![]() ≤
≤![]() .∴
.∴![]() ≤λ<1或1<λ≤5.
≤λ<1或1<λ≤5.

练习册系列答案
相关题目
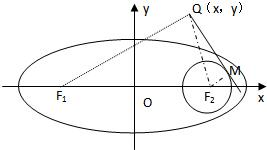 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: