题目内容
已知函数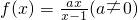 .
.
(1)判断函数f(x)在(-1,1)上的单调性,并用单调性的定义加以证明;
(2)若a=1,求函数f(x)在 上的值域.
上的值域.
解:(1)当a>0时,设-1<x1<x2<1
 =
= =
=
∵x1-1<0,x2-1<0,a(x1-x2)<0
∴ >0,得f(x1)>f(x2),函数f(x)在(-1,1)上是减函数;
>0,得f(x1)>f(x2),函数f(x)在(-1,1)上是减函数;
同理可得,当a<0时,函数f(x)在(-1,1)上是增函数.
(2)当a=1时,由(1)得f(x)= 在(-1,1)上是减函数
在(-1,1)上是减函数
∴函数f(x在 上也是减函数,其最小值为f(
上也是减函数,其最小值为f( )=-1,最大值为f(-
)=-1,最大值为f(- )=
)=
由此可得,函数f(x)在 上的值域为[-1,
上的值域为[-1, ].
].
分析:(1)根据单调性的定义,进行作差变形整理,可得当a>0时,函数f(x)在(-1,1)上是减函数,当a<0时,函数f(x)在(-1,1)上是增函数;
(2)根据(1)的单调性,算出函数在在 上的最大值和最小值,由此即可得到f(x)在
上的最大值和最小值,由此即可得到f(x)在 上的值域.
上的值域.
点评:本题给出分式函数,讨论了函数的单调性并求函数在闭区间上的值域,着重考查了函数单调性的判断与证明和函数的值域等知识,属于基础题.
 =
= =
=
∵x1-1<0,x2-1<0,a(x1-x2)<0
∴
 >0,得f(x1)>f(x2),函数f(x)在(-1,1)上是减函数;
>0,得f(x1)>f(x2),函数f(x)在(-1,1)上是减函数;同理可得,当a<0时,函数f(x)在(-1,1)上是增函数.
(2)当a=1时,由(1)得f(x)=
 在(-1,1)上是减函数
在(-1,1)上是减函数∴函数f(x在
 上也是减函数,其最小值为f(
上也是减函数,其最小值为f( )=-1,最大值为f(-
)=-1,最大值为f(- )=
)=
由此可得,函数f(x)在
 上的值域为[-1,
上的值域为[-1, ].
].分析:(1)根据单调性的定义,进行作差变形整理,可得当a>0时,函数f(x)在(-1,1)上是减函数,当a<0时,函数f(x)在(-1,1)上是增函数;
(2)根据(1)的单调性,算出函数在在
 上的最大值和最小值,由此即可得到f(x)在
上的最大值和最小值,由此即可得到f(x)在 上的值域.
上的值域.点评:本题给出分式函数,讨论了函数的单调性并求函数在闭区间上的值域,着重考查了函数单调性的判断与证明和函数的值域等知识,属于基础题.

练习册系列答案
相关题目

 ,
, 上的单调性;
上的单调性; .
. ,求a,b的值.
,求a,b的值. .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分) ,记
,记 ,试求函数
,试求函数 在区间
在区间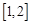 上的最大值.(10分)
上的最大值.(10分) .
. ,
, 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间