题目内容
若一球的半径为r，作内接于球的圆柱，则其侧面积最大为（ ）A.2πr2
B.πr2
C.4πr2
D.
πr2
解析：作出截面图,则圆柱的底面半径为rcosθ,高为2rcosθ.故侧面积为2πrcosθ·2rsinθ= 2πr2sin2θ,∴最大值为2πr2.选A.
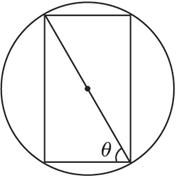
答案：A
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
若一球的半径为r，作内接于球的圆柱，则其侧面积最大为（ ）A.2πr2
B.πr2
C.4πr2
D.πr2
解析：作出截面图,则圆柱的底面半径为rcosθ,高为2rcosθ.故侧面积为2πrcosθ·2rsinθ= 2πr2sin2θ,∴最大值为2πr2.选A.
答案：A
天天向上一本好卷系列答案小学生10分钟应用题系列答案
πr2
πr2
πr2