题目内容
椭圆E的中心在坐标原点,焦点在x轴上,离心率为 .点P(1,
.点P(1, )、A、B在椭圆E上,且
)、A、B在椭圆E上,且
 =m
=m (m∈R)
(m∈R)
(Ⅰ)求椭圆E的方程.
(Ⅱ)当m=-3时,求△PAB的重心坐标.
(Ⅲ)证明直线AB的斜率为定值,并求出这个定值.
(Ⅰ)解:设椭圆方程为 +
+ =1(a>b>0)
=1(a>b>0)
∵椭圆的离心率为 ,点P(1,
,点P(1, )在椭圆E上,
)在椭圆E上,
∴e2=1- =
= 及
及 +
+ =1
=1
∴a2=4,b2=3,
∴椭圆方程为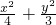 =1;
=1;
(Ⅱ)解:设A(x1,y1)、B(x2,y2),由
 =m
=m
得(x1+x2-2,y1+y2-3)=m(1, ),即
),即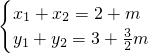
∵点P(1, ),),m=-3,于是x1+x2+1=3+m=0,y1+y2+
),),m=-3,于是x1+x2+1=3+m=0,y1+y2+ =3+
=3+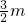 +
+ =0,
=0,
因此△PAB的重心坐标为(0,0),即原点是△PAB的重心;
(Ⅲ)证明:∵ =1,
=1, =1
=1
∴两式相减得kAB= =-
=- ×
× =
= =-
=- ,即直线AB的斜率为定值,定值为-
,即直线AB的斜率为定值,定值为- .
.
分析:(Ⅰ)设椭圆方程,利用椭圆的离心率为 ,点P(1,
,点P(1, )在椭圆E上,建立方程求得几何量,即可求得椭圆方程;
)在椭圆E上,建立方程求得几何量,即可求得椭圆方程;
(Ⅱ)设A、B的坐标,由
 =m
=m 得坐标之间的关系,即可求得△PAB的重心坐标;
得坐标之间的关系,即可求得△PAB的重心坐标;
(Ⅲ)利用点差法,结合(Ⅱ)的结论,即可得到结论.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查点差法求直线的斜率,正确运用椭圆方程是关键.
 +
+ =1(a>b>0)
=1(a>b>0)∵椭圆的离心率为
 ,点P(1,
,点P(1, )在椭圆E上,
)在椭圆E上,∴e2=1-
 =
= 及
及 +
+ =1
=1∴a2=4,b2=3,
∴椭圆方程为
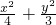 =1;
=1;(Ⅱ)解:设A(x1,y1)、B(x2,y2),由

 =m
=m
得(x1+x2-2,y1+y2-3)=m(1,
 ),即
),即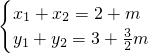
∵点P(1,
 ),),m=-3,于是x1+x2+1=3+m=0,y1+y2+
),),m=-3,于是x1+x2+1=3+m=0,y1+y2+ =3+
=3+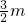 +
+ =0,
=0,因此△PAB的重心坐标为(0,0),即原点是△PAB的重心;
(Ⅲ)证明:∵
 =1,
=1, =1
=1∴两式相减得kAB=
 =-
=- ×
× =
= =-
=- ,即直线AB的斜率为定值,定值为-
,即直线AB的斜率为定值,定值为- .
.分析:(Ⅰ)设椭圆方程,利用椭圆的离心率为
 ,点P(1,
,点P(1, )在椭圆E上,建立方程求得几何量,即可求得椭圆方程;
)在椭圆E上,建立方程求得几何量,即可求得椭圆方程;(Ⅱ)设A、B的坐标,由

 =m
=m 得坐标之间的关系,即可求得△PAB的重心坐标;
得坐标之间的关系,即可求得△PAB的重心坐标;(Ⅲ)利用点差法,结合(Ⅱ)的结论,即可得到结论.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查点差法求直线的斜率,正确运用椭圆方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目