题目内容
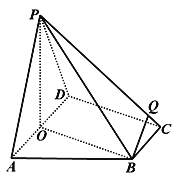
【题目】如图，四棱锥中
，底面
为直角梯形，
，
，平面
底面，
，
.
（Ⅰ）判断平面
与平面
是否垂直，并给出证明；
（Ⅱ）若
，
，
，求二面角
的余弦值.
【答案】（Ⅰ）见证明；（Ⅱ）
【解析】
（Ⅰ）利用反证法证明，假设面PBC⊥面PCD，过点B作BQ⊥PC于Q，由面面垂直的性质可得BQ⊥CD，知BC⊥CD，则CD⊥PC，由平面
底面
，则CD⊥PD，出现矛盾；（Ⅱ）取AD中点O，连PO，OB，证明OA、OB、OP两两互相垂直，以OA、OB、OP所在直线分别为x、y、z轴建立如空间直角坐标系O﹣xyz，分别求面PAB与面PBC的法向量，由两法向量所成角余弦值可得二面角A﹣PB﹣C余弦值．
（Ⅰ）平面
与平面
不垂直.证明如下：
假设平面
平面，过点
作
于
∵平面平面，平面
平面
∴
平面
∴
在直角梯形中，由
，
知
又∵
∴ 
平面，故
∵ 平面底面，平面
底面
，
∴ 
平面
∴ 
在
中，不可能有两个直角，所以假设不成立
（Ⅱ）设
的中点为
，连接
，
∵
∴
∵ 平面底面，平面底面
∴
底面
∵在直角梯形中，，
∴
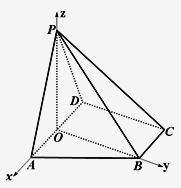
以
、、
所在直线分别为
、
、
轴建立如图所示空间直角坐标系
∵
，
，
∴
，
，
，
∴
，
，
，
设平面
的法向量为
由
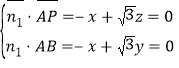， 取
同理可得平面的法向量
∴
.
由图形可知，所求二面角为钝角
∴二面角
的余弦值
练习册系列答案
备战中考寒假系列答案
相关题目
