题目内容
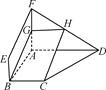
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD =" EF" = 1.
(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE的值.
(1)(2)见解析(3)
解析试题分析:(1)要证 ,则需要证明
,则需要证明 与平面
与平面 内的两条相交直线垂直,而根据题意已知
内的两条相交直线垂直,而根据题意已知 ,故只需再根据题意平面
,故只需再根据题意平面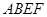 ⊥平面
⊥平面 ,可证
,可证 ,从而证明
,从而证明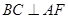 ,则可证明结论.
,则可证明结论.
(2)要证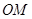 ∥平面
∥平面 ,则需要在平面
,则需要在平面 内找一条直线与
内找一条直线与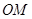 平行,根据点
平行,根据点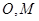 都是中点的特点, 取
都是中点的特点, 取 中点
中点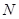 ,证明四边形
,证明四边形 为平行四边形,即有
为平行四边形,即有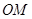 ∥
∥ ,则可证明结论.
,则可证明结论.
(3)要求体积比,首先得找到体积,根据题意可知,分割后形成了两个棱锥,一个四棱锥,一个三棱锥;根据棱锥的体积公式,得找到底面积和高,而其中四棱锥的底面和高比较容易确定,而三棱锥中关键是确定底面和高,确定的依据就是是否有现成的线面垂直,显然 ,所以确定底面为
,所以确定底面为 高
高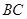 .最后分别求体积做比值即可.
.最后分别求体积做比值即可.
试题解析:(1) 平面
平面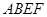 ⊥平面
⊥平面 ,平面
,平面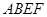
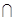 平面
平面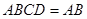 ,
,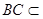 平面
平面 ,而四边形
,而四边形 为矩形
为矩形 ,
,
.
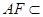 平面
平面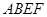
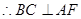
则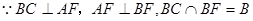 ,
,
(2)取 中点
中点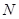 ,连接
,连接 ,则
,则 ∥
∥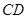 ,且
,且 ,又四边形
,又四边形 为矩形,
为矩形,
 ∥
∥ ,且
,且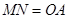
 四边形
四边形 为平行四边形,
为平行四边形,
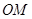 ∥
∥
又
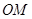
 平面
平面 ,
,
 平面
平面

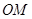 ∥平面
∥平面
(3)过 作
作 于
于 ,由题意可得:
,由题意可得:
 平面
平面 .
.
所以: .
.
因为 平面
平面

练习册系列答案
相关题目
 中,
中, ,
, ,
, 为正三角形,且平面
为正三角形,且平面 平面
平面 .
.
 ;
; 的余弦值.
的余弦值. 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中 ,
, ,平面
,平面 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
;
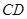 ;
; 与平面
与平面 所成角的正弦值。
所成角的正弦值。 都为正方形,
都为正方形, ,F
,F 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.
 平面AEF;
平面AEF;
 平面;
平面; ,写出
,写出 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明). 中,侧面
中,侧面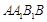 为菱形,且
为菱形,且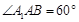 ,
, ,
,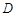 是
是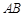 的中点.
的中点.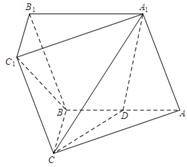
 平面
平面 ;
; ∥平面
∥平面 .
. 于
于 (不同于点
(不同于点 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥 ,如图2所示.
,如图2所示.
 //平面
//平面 ;
; ;
; 平面
平面 ,试判断直线
,试判断直线 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由. ,
,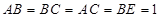 ,
,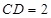 ,
,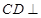 平面
平面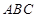 ,
,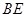 ∥
∥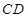 ,
,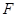 为
为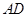 的中点.
的中点.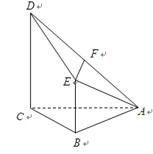
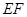 ∥平面
∥平面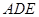
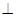 平面
平面 ;
; ABCD中,底面是边长为2
ABCD中,底面是边长为2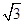 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2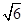 ,M、N分别为PB、PD的中点.
,M、N分别为PB、PD的中点.
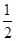 AD,BE∥=
AD,BE∥=