题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c,且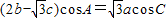 .
.(Ⅰ)求角A的大小;
(Ⅱ)若
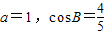 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(1)由已知结合正弦定理可求cosA,进而可求A
(2)由cosB结合同角平方关系可求sinB,然后利用诱导公式及两角和的 正弦公式sinC=sin(A+B)=sinAcosB+sinBcosA可求sinC,然后由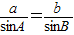 可求 b,代入三角形的面积公式
可求 b,代入三角形的面积公式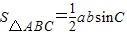 可求
可求
解答:解:(1)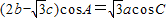
∴(2sinB-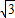 cosC)cosA=
cosC)cosA=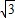 sinAcosC
sinAcosC
即2sinBcosA=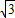 sinAcosC+
sinAcosC+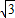 sinCcosA
sinCcosA
∴2sinBcosA=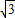 sin(A+C)
sin(A+C)
则2sinBcosA=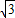 sinB
sinB
∵sinB≠0
∴cosA=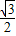
∵0<A<π
则A=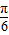
(2)由cosB= 可得sinB=
可得sinB=
又cosA=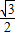 ,sinA=
,sinA=
∴sinC=sin(A+B)=sinAcosB+sinBcosA=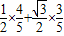 =
=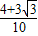
由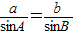 可得b=
可得b=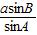 =
=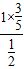 =
=
∴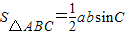 =
=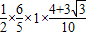 =
=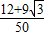
点评:本题主要考查了正弦定理、同角平方关系、诱导公式及两角和的正弦公式、三角形的面积公式等知识的综合应用,解题的关键是灵活利用公式
(2)由cosB结合同角平方关系可求sinB,然后利用诱导公式及两角和的 正弦公式sinC=sin(A+B)=sinAcosB+sinBcosA可求sinC,然后由
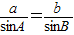 可求 b,代入三角形的面积公式
可求 b,代入三角形的面积公式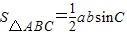 可求
可求解答:解:(1)
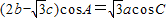
∴(2sinB-
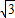 cosC)cosA=
cosC)cosA=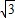 sinAcosC
sinAcosC即2sinBcosA=
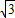 sinAcosC+
sinAcosC+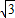 sinCcosA
sinCcosA∴2sinBcosA=
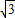 sin(A+C)
sin(A+C)则2sinBcosA=
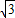 sinB
sinB∵sinB≠0
∴cosA=
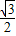
∵0<A<π
则A=
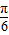
(2)由cosB=
 可得sinB=
可得sinB=
又cosA=
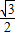 ,sinA=
,sinA=
∴sinC=sin(A+B)=sinAcosB+sinBcosA=
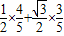 =
=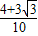
由
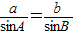 可得b=
可得b=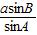 =
=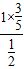 =
=
∴
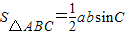 =
=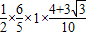 =
=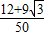
点评:本题主要考查了正弦定理、同角平方关系、诱导公式及两角和的正弦公式、三角形的面积公式等知识的综合应用,解题的关键是灵活利用公式

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目