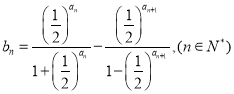题目内容
【题目】函数![]() 在一个周期内的图象如图所示,A为图象的最高点,B,C为
在一个周期内的图象如图所示,A为图象的最高点,B,C为![]() 的图象与x轴的交点,且
的图象与x轴的交点,且![]() 为等边三角形.将函数
为等边三角形.将函数![]() 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的![]() 倍后,再向右平移
倍后,再向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.

(1)求函数![]() 的解析式;
的解析式;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意结合平面几何的知识可得![]() ,再由
,再由![]() 即可得
即可得![]() ,再利用三角函数图象变换的规律即可得解;
,再利用三角函数图象变换的规律即可得解;
(2)由题意结合诱导公式、同角三角函数平方关系转化条件得![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,按照
,按照![]() 、
、![]() 、
、![]() 分类,结合二次函数的性质即可得解.
分类,结合二次函数的性质即可得解.
(1)由题意点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() 为等边三角形,
为等边三角形,
所以三角形边长为2,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
将函数![]() 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的![]() 倍后,得到
倍后,得到![]() ,
,
再向右平移![]() 个单位,得到
个单位,得到![]() ;
;
(2)由题意![]() ,
,
所以![]() 恒成立,
恒成立,
原不等式等价于![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,对称轴
,对称轴![]() ,
,
当![]() 时,
时,![]() 成立;
成立;
当![]() 时,
时,![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
综上,实数m的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: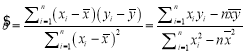 ,
,![]() .
.
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料。试求:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
⑴画出数据的散点图,并判断y与x是否呈线性相关关系.
⑵若y与x呈线性相关关系,求线性回归方程 y = bx + a 的回归系数a、b;
⑶估计使用年限为10年时,维修费用是多少?
(参考数据: ,
,![]() ,
,![]() ,
,![]() )
)