题目内容
如图,已知直线L:x=my+1过椭圆C:![]() (a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.

(1)若抛物线x2=4![]() y的焦点为椭圆C的上顶点,求椭圆C的方程;
y的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)(理)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由.
(文)若N(![]() )为x轴上一点,求证:
)为x轴上一点,求证:![]()
答案:
解析:
解析:
|
先探索,当m=0时,直线L⊥ox轴,则ABED为矩形,由对称性知,AE与BD相交于FK中点N,且 猜想:当m变化时,AE与BD相交于定点 证明:设 当m变化时首先AE过定点N ∴KAN=KEN ∴A、N、E三点共线 同理可得B、N、D三点共线 |

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目




 如图,已知直线l:x=my+1过椭圆
如图,已知直线l:x=my+1过椭圆 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2. 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: (2012•乐山二模)如图,已知直线L:x=my+1过椭圆C:
(2012•乐山二模)如图,已知直线L:x=my+1过椭圆C: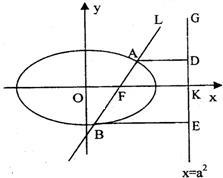 如图,已知直线L:
如图,已知直线L: