题目内容
当x>0时, 的单调减区间是
的单调减区间是
- A.(2,+∞)
- B.(0,2)
- C.
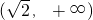
- D.
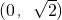
B
分析:由已知中函数的解析式,我们可以求出其导函数的解析式,根据导函数在函数的单调递减区间上函数值小于0,我们可以构造一个关于x的不等式,解不等式,即可求出满足条件的x的取值范围,得到答案.
解答:∵函数 ,(x>0)
,(x>0)
∴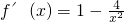 ,(x>0)
,(x>0)
令y′>0,即 <0
<0
解得0<x<2
故函数 ,(x>0)单调减区间是(0,2)
,(x>0)单调减区间是(0,2)
故选B
点评:本题考查的知识点是函数的单调性及单调区间,函数的单调性的判断与证明,其中根据导函数在函数的单调递减区间上函数值小于0,构造一个关于x的不等式,是解答本题的关键.
分析:由已知中函数的解析式,我们可以求出其导函数的解析式,根据导函数在函数的单调递减区间上函数值小于0,我们可以构造一个关于x的不等式,解不等式,即可求出满足条件的x的取值范围,得到答案.
解答:∵函数
 ,(x>0)
,(x>0)∴
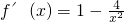 ,(x>0)
,(x>0)令y′>0,即
 <0
<0解得0<x<2
故函数
 ,(x>0)单调减区间是(0,2)
,(x>0)单调减区间是(0,2)故选B
点评:本题考查的知识点是函数的单调性及单调区间,函数的单调性的判断与证明,其中根据导函数在函数的单调递减区间上函数值小于0,构造一个关于x的不等式,是解答本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 的单调减区间是( )
的单调减区间是( )
