题目内容
已知函数 (x∈R且x≠0)
(x∈R且x≠0)
(1)判断f(x)的奇偶性;
(2)当x>0时,用单调性的定义讨论并求出函数f(x)的单调增区间和单调减区间.
解:(1)函数f(x)为奇函数,理由如下:
∵函数 (x∈R且x≠0)
(x∈R且x≠0)
∴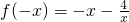 =-f(x)
=-f(x)
∴函数f(x)为奇函数,
(2)当x>0时,区间(0,2]为函数 的单调递减区间,
的单调递减区间,
区间[2,+∝)为函数 的单调递增区间,
的单调递增区间,
理由如下:
∵
∴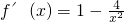
当0<x≤2时,f′(x)≤0恒成立,此时函数为减函数;
当x≥2时,f′(x)≥0恒成立,此时函数为增函数;
分析:(1)根据已知中函数的定义域关于原点对称,故我们只要判断f(-x)与f(x)的关系,进而根据函数奇偶性的定义,即可判断出f(x)的奇偶性;
(2)根据已知中函数 的解析式,我们可以求出其导函数的解析式,进而根据导函数值大于0,函数为增函数,导函数值小于0,函数为减函数,得到当x>0时,函数f(x)的单调增区间和单调减区间.
的解析式,我们可以求出其导函数的解析式,进而根据导函数值大于0,函数为增函数,导函数值小于0,函数为减函数,得到当x>0时,函数f(x)的单调增区间和单调减区间.
点评:本题考查的知识点是函数奇偶性的判断,函数单调性的判断与证明,其中熟练掌握函数单调性和奇偶性的方法和步骤是解答此类问题的关键.
∵函数
 (x∈R且x≠0)
(x∈R且x≠0)∴
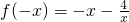 =-f(x)
=-f(x)∴函数f(x)为奇函数,
(2)当x>0时,区间(0,2]为函数
 的单调递减区间,
的单调递减区间,区间[2,+∝)为函数
 的单调递增区间,
的单调递增区间,理由如下:
∵

∴
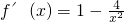
当0<x≤2时,f′(x)≤0恒成立,此时函数为减函数;
当x≥2时,f′(x)≥0恒成立,此时函数为增函数;
分析:(1)根据已知中函数的定义域关于原点对称,故我们只要判断f(-x)与f(x)的关系,进而根据函数奇偶性的定义,即可判断出f(x)的奇偶性;
(2)根据已知中函数
 的解析式,我们可以求出其导函数的解析式,进而根据导函数值大于0,函数为增函数,导函数值小于0,函数为减函数,得到当x>0时,函数f(x)的单调增区间和单调减区间.
的解析式,我们可以求出其导函数的解析式,进而根据导函数值大于0,函数为增函数,导函数值小于0,函数为减函数,得到当x>0时,函数f(x)的单调增区间和单调减区间.点评:本题考查的知识点是函数奇偶性的判断,函数单调性的判断与证明,其中熟练掌握函数单调性和奇偶性的方法和步骤是解答此类问题的关键.

练习册系列答案
相关题目

 (x>-2),求此函数的最小值.
(x>-2),求此函数的最小值. ,求y=4x-1+
,求y=4x-1+ 的最大值;
的最大值; 的最小值.
的最小值.