题目内容
已知函数y=a2x+2ax-1(a>0且a≠1)在[-1,1]上的最大值是14.
(1)求a的值;
(2)求函数y=a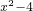 的单调区间.
的单调区间.
解:(1)令t=ax,则y=t2+2t-1=(t+1)2-2,
当a>1时,∵x∈[-1,1],则t∈[ ,a],
,a],
∴函数在[ ,a]上是增函数,
,a]上是增函数,
∴当t=a时,函数取到最大值14=a2+2a-1,
解得a=3或-5(舍),则a的值为3.
若0<a<1,则t=ax是减函数,所以>a
所以0<a<t<a-1
所以y的图象都在对称轴t=-1的右边,开口向上 并且递增
所以t=a-1时有最大值
所以y=(a-1+1)2-2=14,解得a= 符合0<a<1
符合0<a<1
故a的值为3或 ;
;
(2)由(1)知, =
= ,
,
则函数 分解成两部分:f(U)=3U外层函数,U=x2-4x 是内层函数.
分解成两部分:f(U)=3U外层函数,U=x2-4x 是内层函数.
根据复合函数的单调性,可得函数y=3U单调增函数,
则函数 单调递增区间就是函数y=x2-4单调递增区间;
单调递增区间就是函数y=x2-4单调递增区间;
函数 单调递减区间就是函数y=x2-4单调递减区间;
单调递减区间就是函数y=x2-4单调递减区间;
∴函数 单调递增区间是(0,+∞),单调递减区间是(-∞,0).
单调递增区间是(0,+∞),单调递减区间是(-∞,0).
分析:(1)由题意令t=ax,则原函数变成关于t的二次函数,求出t的范围,根据在区间上的单调性求出函数有最大值时对应的t值,进而求出a的值.
(2)由(1)知, =
= ,依据复合函数的单调性来判断,即可得到
,依据复合函数的单调性来判断,即可得到 的单调区间.
的单调区间.
点评:本小题主要考查复合函数单调性的应用、二次函数单调性的应用、不等式的解法及函数的最值问题等基础知识,考查运算求解能力与转化思想.属于基础题.
当a>1时,∵x∈[-1,1],则t∈[
 ,a],
,a],∴函数在[
 ,a]上是增函数,
,a]上是增函数,∴当t=a时,函数取到最大值14=a2+2a-1,
解得a=3或-5(舍),则a的值为3.
若0<a<1,则t=ax是减函数,所以>a
所以0<a<t<a-1
所以y的图象都在对称轴t=-1的右边,开口向上 并且递增
所以t=a-1时有最大值
所以y=(a-1+1)2-2=14,解得a=
 符合0<a<1
符合0<a<1故a的值为3或
 ;
;(2)由(1)知,
 =
= ,
,则函数
 分解成两部分:f(U)=3U外层函数,U=x2-4x 是内层函数.
分解成两部分:f(U)=3U外层函数,U=x2-4x 是内层函数.根据复合函数的单调性,可得函数y=3U单调增函数,
则函数
 单调递增区间就是函数y=x2-4单调递增区间;
单调递增区间就是函数y=x2-4单调递增区间;函数
 单调递减区间就是函数y=x2-4单调递减区间;
单调递减区间就是函数y=x2-4单调递减区间;∴函数
 单调递增区间是(0,+∞),单调递减区间是(-∞,0).
单调递增区间是(0,+∞),单调递减区间是(-∞,0).分析:(1)由题意令t=ax,则原函数变成关于t的二次函数,求出t的范围,根据在区间上的单调性求出函数有最大值时对应的t值,进而求出a的值.
(2)由(1)知,
 =
= ,依据复合函数的单调性来判断,即可得到
,依据复合函数的单调性来判断,即可得到 的单调区间.
的单调区间.点评:本小题主要考查复合函数单调性的应用、二次函数单调性的应用、不等式的解法及函数的最值问题等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目