题目内容
设函数f（x）=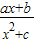
的图象如图所示，则a、b、c的大小关系是（ ）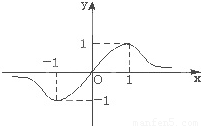
A．a＞b＞c
B．a＞c＞b
C．b＞a＞c
D．c＞a＞b
【答案】分析：由函数图象可得f（0）=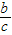
=0，解得b=0，又f（1）=
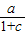=1，故a=c+1，再由f′（1）=0，可得c的值，进而可得a的值，故可比较大小．
解答：解：由函数图象可得f（0）=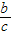
=0，解得b=0，
又f（1）=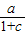
=1，故a=c+1，
又f′（x）=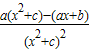
=
，
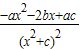由图可知x=1为函数的极值点，故f′（1）=0，
即-a+ac=0，解得c=1，a=2，
故a＞c＞b，
故选B
点评：本题考查由函数的图象求解函数的系数的问题，属基础题．
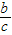=0，解得b=0，又f（1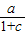）==1，故a=c+1，再由f′（1）=0，可得c的值，进而可得a的值，故可比较大小．解答：解：由函数图象可得f（0）=
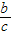=0，解得b=0，又f（1）=
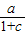=1，故a=c+1，又f′（x）=
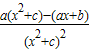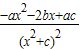=，由图可知x=1为函数的极值点，故f′（1）=0，
即-a+ac=0，解得c=1，a=2，
故a＞c＞b，
故选B
点评：本题考查由函数的图象求解函数的系数的问题，属基础题．
练习册系列答案
口算能手系列答案
相关题目
设函数f（x）=asinx-bcosx图象的一条对称轴方程为x=
，则直线ax-by+c=0的倾斜角为（ ）
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|