题目内容
(2012•茂名一模)已知函数f(x)=lnx的图象是曲线C,点An(an,f(an))(n∈N*)是曲线C上的一系列点,曲线C在点An(an,f(an))处的切线与y轴交于点Bn(0,bn),若数列{bn}是公差为2的等差数列,且f(a1)=3.
(1)分别求出数列{an}与数列{bn}的通项公式;
(2)设O为坐标原点,Sn表示△AnBn的面积,求数列{Sn}的前n项和Tn.
(1)分别求出数列{an}与数列{bn}的通项公式;
(2)设O为坐标原点,Sn表示△AnBn的面积,求数列{Sn}的前n项和Tn.
分析:(1)求导函数,确定曲线C在点An(an,f(an))处的切线方程,令x=0,可得bn=lnan-1,利用数列{bn}是公差为2的等差数列,可得
=e2,根据f(a1)=3,可得a1=e3,由此即可求得数列的通项;
(2)Sn=
×bn×an=n×e2n+1,Tn=1×e3+2×e5+…+n×e2n+1,利用错位相减法即可求和.
| an+1 |
| an |
(2)Sn=
| 1 |
| 2 |
解答:解:(1)求导函数可得f′(x)=
,则曲线C在点An(an,f(an))处的切线方程为y-lnan=
(x-an)
令x=0,则y-lnan=-1,∴bn=lnan-1
∴bn+1-bn=lnan+1-1-lnan+1=2
∴
=e2
∵f(a1)=3,
∴ln(a1)=3,
∴a1=e3,
∴an=e2n+1
∴bn=lnan-1=2n;
(2)Sn=
×bn×an=n×e2n+1
∴Tn=1×e3+2×e5+…+n×e2n+1①
∴e2Tn=1×e5+2×e7+…+(n-1)×e2n+1+n×e2n+3②
①-②可得Tn-e2Tn=1×e3+1×e5+…+1×e2n+1-n×e2n+3
∴Tn=
-
| 1 |
| x |
| 1 |
| an |
令x=0,则y-lnan=-1,∴bn=lnan-1
∴bn+1-bn=lnan+1-1-lnan+1=2
∴
| an+1 |
| an |
∵f(a1)=3,
∴ln(a1)=3,
∴a1=e3,
∴an=e2n+1
∴bn=lnan-1=2n;
(2)Sn=
| 1 |
| 2 |
∴Tn=1×e3+2×e5+…+n×e2n+1①
∴e2Tn=1×e5+2×e7+…+(n-1)×e2n+1+n×e2n+3②
①-②可得Tn-e2Tn=1×e3+1×e5+…+1×e2n+1-n×e2n+3
∴Tn=
| e3-e3+2n |
| (1-e2)2 |
| n×e2n+3 |
| 1-e2 |
点评:本题考查数列与函数的结合,考查数列的通项,考查数列的求和,解题的关键是确定数列的通项,利用错位相减法求数列的和.

练习册系列答案
相关题目
 (2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
(2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: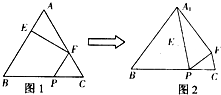 (2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).
(2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2). (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且