题目内容
等比数列首项a>0,公比q>0,前n项和为80,其中最大的一项为54,又它的前2n项和为6560,则a= ,q= .
【答案】分析:由题意可得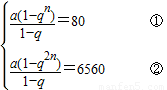 解得 qn=81. 再由q>0,可得q>1.又a>0,故该数列为递增数列.设前n项中最大的项为an,可得an=aqn-1=54,
解得 qn=81. 再由q>0,可得q>1.又a>0,故该数列为递增数列.设前n项中最大的项为an,可得an=aqn-1=54,
又qn=81,∴3a=2q,将qn=81代入①得a=q-1,由此求得a、q的值.
解答:解:由Sn=80,S2n=6560知q≠1,∴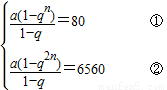 解得 qn=81.
解得 qn=81.
∵q>0,∴q>1,又a>0,∴该数列为递增数列.
设前n项中最大的项为an,∴an=aqn-1=54,又qn=81,∴3a=2q,将qn=81代入①得a=q-1,
∴a=2,q=3,
故答案为 2;3.
点评:本题主要考查等比数列的通项公式以及前n项和公式的应用,属于中档题.
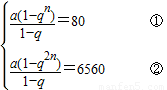 解得 qn=81. 再由q>0,可得q>1.又a>0,故该数列为递增数列.设前n项中最大的项为an,可得an=aqn-1=54,
解得 qn=81. 再由q>0,可得q>1.又a>0,故该数列为递增数列.设前n项中最大的项为an,可得an=aqn-1=54,又qn=81,∴3a=2q,将qn=81代入①得a=q-1,由此求得a、q的值.
解答:解:由Sn=80,S2n=6560知q≠1,∴
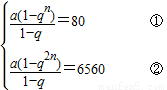 解得 qn=81.
解得 qn=81. ∵q>0,∴q>1,又a>0,∴该数列为递增数列.
设前n项中最大的项为an,∴an=aqn-1=54,又qn=81,∴3a=2q,将qn=81代入①得a=q-1,
∴a=2,q=3,
故答案为 2;3.
点评:本题主要考查等比数列的通项公式以及前n项和公式的应用,属于中档题.

练习册系列答案
相关题目