题目内容
已知 ,且
,且 ,则sinα+cosα的值是
,则sinα+cosα的值是
- A.

- B.
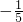
- C.

- D.

B
分析:由α的范围求出 的范围,把所求式子提取
的范围,把所求式子提取 ,利用两角和的正弦函数公式及特殊角的三角函数值化为关于
,利用两角和的正弦函数公式及特殊角的三角函数值化为关于 的正弦函数,根据正弦函数的图象与性质得到所求式子小于0,然后根据同角三角函数的基本关系用sinαcosα表示出所求的式子,把sinαcosα的值代入即可得出所求式子的值.
的正弦函数,根据正弦函数的图象与性质得到所求式子小于0,然后根据同角三角函数的基本关系用sinαcosα表示出所求的式子,把sinαcosα的值代入即可得出所求式子的值.
解答:∵ ,∴
,∴ ∈(π,
∈(π, ),
),
∴sinα+cosα= sin(
sin( )<0,又
)<0,又 ,
,
则sinα+cosα=- =
= =-
=- .
.
故选B
点评:本题考查同角三角函数的基本关系的运用,解题的关系是熟练掌握同角三角函数的几个关系:平方关系,商数关系等,本题主要是利用平方关系变化求值.
分析:由α的范围求出
 的范围,把所求式子提取
的范围,把所求式子提取 ,利用两角和的正弦函数公式及特殊角的三角函数值化为关于
,利用两角和的正弦函数公式及特殊角的三角函数值化为关于 的正弦函数,根据正弦函数的图象与性质得到所求式子小于0,然后根据同角三角函数的基本关系用sinαcosα表示出所求的式子,把sinαcosα的值代入即可得出所求式子的值.
的正弦函数,根据正弦函数的图象与性质得到所求式子小于0,然后根据同角三角函数的基本关系用sinαcosα表示出所求的式子,把sinαcosα的值代入即可得出所求式子的值.解答:∵
 ,∴
,∴ ∈(π,
∈(π, ),
),∴sinα+cosα=
 sin(
sin( )<0,又
)<0,又 ,
,则sinα+cosα=-
 =
= =-
=- .
.故选B
点评:本题考查同角三角函数的基本关系的运用,解题的关系是熟练掌握同角三角函数的几个关系:平方关系,商数关系等,本题主要是利用平方关系变化求值.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 cos
cos ,且
,且 ,则sin
,则sin B.
-
B.
-

 ,且
,且 ,则sinα= .
,则sinα= . ,且
,且 ,则sinα=( )
,则sinα=( )



 ,且
,且 ,则sinα= .
,则sinα= . ,且
,且 ,则sinα的值为( )
,则sinα的值为( )


