题目内容
已知函数 ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期和值域;
(2)求函数f(x)的单调增区间.
解:(1)∵ =
= =
= ,
,
∴函数f(x)的最小正周期 ,又∵x∈R,∴
,又∵x∈R,∴ ,
,
∴ ,∴函数f(x)的值域为 {y|-2≤y≤2}.
,∴函数f(x)的值域为 {y|-2≤y≤2}.
(2)由 ,k∈Z,得
,k∈Z,得 ,k∈Z,
,k∈Z,
∴函数f(x)的单调增区间为 .
.
分析:(1)利用两角和正弦公式化简函数f(x)的解析式,求出周期,由 ,求得函数f(x)的值域.
,求得函数f(x)的值域.
(2)由 ,k∈Z,求得
,k∈Z,求得 ,k∈Z,即得函数的单调增区间.
,k∈Z,即得函数的单调增区间.
点评:本题考查两角和正弦公式,正弦函数的单调性,周期性,和值域,化简函数f(x)的解析式,是解题的突破口.
 =
= =
= ,
,∴函数f(x)的最小正周期
 ,又∵x∈R,∴
,又∵x∈R,∴ ,
,∴
 ,∴函数f(x)的值域为 {y|-2≤y≤2}.
,∴函数f(x)的值域为 {y|-2≤y≤2}.(2)由
 ,k∈Z,得
,k∈Z,得 ,k∈Z,
,k∈Z,∴函数f(x)的单调增区间为
 .
.分析:(1)利用两角和正弦公式化简函数f(x)的解析式,求出周期,由
 ,求得函数f(x)的值域.
,求得函数f(x)的值域.(2)由
 ,k∈Z,求得
,k∈Z,求得 ,k∈Z,即得函数的单调增区间.
,k∈Z,即得函数的单调增区间.点评:本题考查两角和正弦公式,正弦函数的单调性,周期性,和值域,化简函数f(x)的解析式,是解题的突破口.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.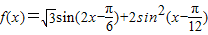 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.