题目内容
(C)已知函数f(x)=|2x+3|+|2x-1|.
(Ⅰ)求不等式f(x)≤6的解集;
(Ⅱ)若关于x的不等式f(x)<|m-1|的解集非空,求实数m的取值范围.
(Ⅰ)求不等式f(x)≤6的解集;
(Ⅱ)若关于x的不等式f(x)<|m-1|的解集非空,求实数m的取值范围.
考点:带绝对值的函数
专题:不等式的解法及应用
分析:(Ⅰ)利用绝对值的几何意义直接求不等式f(x)≤6的解集;
(Ⅱ)求出函数的最小值,然后求解关于x的不等式f(x)<|m-1|的解集非空,得到实数m的取值范围.
(Ⅱ)求出函数的最小值,然后求解关于x的不等式f(x)<|m-1|的解集非空,得到实数m的取值范围.
解答:
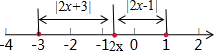 解:(Ⅰ)不等式f(x)≤6,即|2x+3|+|2x-1|≤6.
解:(Ⅰ)不等式f(x)≤6,即|2x+3|+|2x-1|≤6.
不等式的几何意义,是数轴是的点2x,到-3与1的距离之和不大于6,
∴-4≤2x≤2,解得-2≤x≤1,
不等式的解集为{x|-2≤x≤1};
(Ⅱ)函数f(x)=|2x+3|+|2x-1|.
由绝对值的几何意义可知:f(x)min≥4,
关于x的不等式f(x)<|m-1|的解集非空,
只须:4<|m-1|,解得m<-3或m>5.
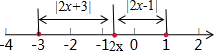 解:(Ⅰ)不等式f(x)≤6,即|2x+3|+|2x-1|≤6.
解:(Ⅰ)不等式f(x)≤6,即|2x+3|+|2x-1|≤6.不等式的几何意义,是数轴是的点2x,到-3与1的距离之和不大于6,
∴-4≤2x≤2,解得-2≤x≤1,
不等式的解集为{x|-2≤x≤1};
(Ⅱ)函数f(x)=|2x+3|+|2x-1|.
由绝对值的几何意义可知:f(x)min≥4,
关于x的不等式f(x)<|m-1|的解集非空,
只须:4<|m-1|,解得m<-3或m>5.
点评:本题考查带绝对值的函数的应用,绝对值不等式的解法,绝对值的几何意义是解题的关键.

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=1,∠ACB=90°,AA1=2,M,N分别是棱CC1,AB中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=1,∠ACB=90°,AA1=2,M,N分别是棱CC1,AB中点.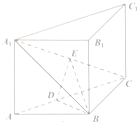 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,AB⊥BC,E是A1C的中点,D在线段AC上,并且DE⊥A1C,已知A1A=AB=
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,AB⊥BC,E是A1C的中点,D在线段AC上,并且DE⊥A1C,已知A1A=AB=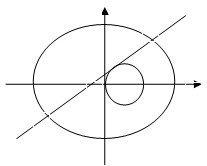 已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,
已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,