题目内容
【题目】椭圆C:![]() +
+![]() =1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=
=1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=![]() ,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,
,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,

(1)求椭圆![]() 的方程和
的方程和![]() 的值;
的值;
(2)若点![]() 坐标为(1,0),过
坐标为(1,0),过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试求
两点,试求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由b=1,离心率e,结合a2﹣b2=c2,求得a和b的值,可得椭圆方程,设点P(x0,y0),则直线B1P方程为y=![]() x﹣1,y=0,得xM=
x﹣1,y=0,得xM=![]() ,同理可得xN=
,同理可得xN=![]() ,即可得解;
,即可得解;
(2)设直线AB的方程为x=ty+1,代入椭圆方程,由韦达定理求得丨y1﹣y2丨=![]() ,S=
,S=![]() 丨MN丨丨y1﹣y2丨,由函数的单调性即可求得△ABN面积的最大值.
丨MN丨丨y1﹣y2丨,由函数的单调性即可求得△ABN面积的最大值.
解:(1)由 ![]() 、
、![]() ,知
,知![]() ,
,
又![]() ,所以
,所以![]() ,
,
则![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() ,
,
设点![]() ,则直线
,则直线![]() 方程为
方程为![]() ,
,
令![]() 得
得![]() ,
,
同理可得![]() ,
,![]() .
.
(2)当点 ![]() 坐标为
坐标为![]() 时,点
时,点![]() ,
,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
代入方程![]() 得
得![]() ,则
,则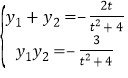
![]()
![]()
![]() ,
,
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
, ![]()
因此当![]() ,即直线
,即直线![]() 的方程为
的方程为![]() 时,
时,
![]() 面积的最大值是
面积的最大值是![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目