题目内容
给出四个函数,则同时具有以下两个性质:①最小正周期是π;②图象关于点(
,0)对称的函数是( )
| π |
| 6 |
A、y=cos(2x-
| ||||
B、y=sin(2x+
| ||||
C、y=sin(
| ||||
D、y=tan(x+
|
分析:利用周期求出ω,再利用图象关于点(
,0)对称,判断选项.
| π |
| 6 |
解答:解:函数最小正周期是π,所以π=
,由选项可知,ω>0,所以ω=2,排除C.
图象关于点(
,0)对称,所以x=
时,函数值为0
显然A,B不满足题意,
+
=
y=tan(x+
)的对称中心是(
,0)
故选D
| 2π |
| |ω| |
图象关于点(
| π |
| 6 |
| π |
| 6 |
显然A,B不满足题意,
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
y=tan(x+
| π |
| 3 |
| π |
| 6 |
故选D
点评:本题考查三角函数的周期性及其求法,正切函数的奇偶性与对称性,考查推理能力,计算能力,是基础题.

练习册系列答案
相关题目
 同时满足:①对任意
同时满足:①对任意 有
有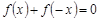 ;②对任意
;②对任意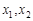 ,当
,当 时,有
时,有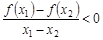 ,则称函数
,则称函数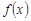 为“理想函数”.给出四个函数:①
为“理想函数”.给出四个函数:① ;②
;② ③
③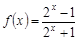 ;④
;④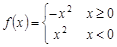 。能被称为“理想函数”的是 .
。能被称为“理想函数”的是 . 同时满足:①对任意
同时满足:①对任意 有
有 ;②对任意
;②对任意 ,当
,当 时,有
时,有 ,则称函数
,则称函数 为“理想函数”.给出四个函数:①
为“理想函数”.给出四个函数:① ;②
;② ③
③ ;④
;④ 。能被称为“理想函数”的是 .
。能被称为“理想函数”的是 . ,0)对称的函数是
,0)对称的函数是 +
+ )
)