题目内容
函数 同时满足:①对任意
同时满足:①对任意 有
有 ;②对任意
;②对任意 ,当
,当 时,有
时,有
 ,则称函数
,则称函数 为“理想函数”.给出四个函数:①
为“理想函数”.给出四个函数:① ;②
;② ③
③ ;④
;④ 。能被称为“理想函数”的是 .
。能被称为“理想函数”的是 .
【答案】
④
【解析】
试题分析:首先根据条件可知,①对任意 有
有 ;②对任意
;②对任意 ,当
,当 时,有
时,有
 ,则称函数
,则称函数 为“理想函数”即说明函数是奇函数,同时在定义域内是减函数,满足题意,由于①
为“理想函数”即说明函数是奇函数,同时在定义域内是减函数,满足题意,由于① 不满足第二个条件,错误;②
不满足第二个条件,错误;② ,不是奇函数,错误。对于③
,不是奇函数,错误。对于③ ;不是减函数错误,对于④
;不是减函数错误,对于④ 结合分段函数图像可知成立,故答案④
结合分段函数图像可知成立,故答案④
考点:函数的单调性和奇偶性
点评:主要是考查了函数单调性和奇偶性的综合运用,属于中档题。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值; ,若同时满足
,若同时满足 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数); ,当
,当 时总有
时总有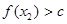 ,则称
,则称 为“平底型”函数。
为“平底型”函数。 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由; ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围; 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。