题目内容
在x轴的正半轴上求一点P,使以A(1,2),B(3,3)及点P为顶点的△ABP的面积为5.
分析:利用以A(1,2),B(3,3)及点P为顶点的△ABP的面积为5,计算出点P到直线AB的距离,利用点到直线的距离公式,即可求得结论.
解答:解:设点P的坐标为(a,0)(a>0),点P到直线AB的距离为d.(2分)
由已知,得S△ABP=
|AB|•d=
•d=5(4分)
解得d=2
(6分)
由已知易得,直线AB的方程为x-2y+3=0(8分)
所以d=
=2
(10分)
解得a=7,或a=-13(舍去)(14分)
所以点P的坐标为(7,0).(15分)
由已知,得S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| (3-1)2+(3-2)2 |
解得d=2
| 5 |
由已知易得,直线AB的方程为x-2y+3=0(8分)
所以d=
| |a+3| | ||
|
| 5 |
解得a=7,或a=-13(舍去)(14分)
所以点P的坐标为(7,0).(15分)
点评:本题考查三角形面积的计算,考查点到直线的距离公式的运用,属于基础题.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
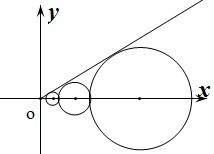
 设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线
设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线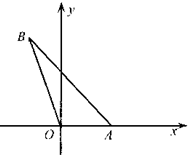 (2010•济宁一模)如图,在平面直角坐标系xoy中,点A在x轴的正半轴上,直线AB的倾斜角为
(2010•济宁一模)如图,在平面直角坐标系xoy中,点A在x轴的正半轴上,直线AB的倾斜角为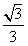 x相切.对每一个正整数n,圆Cn都与圆Cn+1,相互外切.以rn表示Cn的半径,已知{rn}为递增数列,
x相切.对每一个正整数n,圆Cn都与圆Cn+1,相互外切.以rn表示Cn的半径,已知{rn}为递增数列,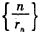 的前n项和.
的前n项和. 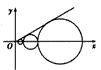
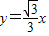 相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.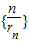 的前n项和.
的前n项和.