题目内容
设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=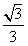 x相切.对每一个正整数n,圆Cn都与圆Cn+1,相互外切.以rn表示Cn的半径,已知{rn}为递增数列,
x相切.对每一个正整数n,圆Cn都与圆Cn+1,相互外切.以rn表示Cn的半径,已知{rn}为递增数列,
(Ⅰ)证明:{rn}为等比数列;
(Ⅱ)设r1=1,求数列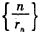 的前n项和.
的前n项和.
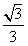 x相切.对每一个正整数n,圆Cn都与圆Cn+1,相互外切.以rn表示Cn的半径,已知{rn}为递增数列,
x相切.对每一个正整数n,圆Cn都与圆Cn+1,相互外切.以rn表示Cn的半径,已知{rn}为递增数列,(Ⅰ)证明:{rn}为等比数列;
(Ⅱ)设r1=1,求数列
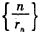 的前n项和.
的前n项和. 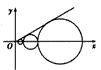
解:(Ⅰ)将直线y=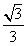 x的倾斜角记为θ,则有
x的倾斜角记为θ,则有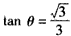 ,
,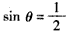 ,
,
设Cn的圆心为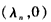 ,
,
则由题意知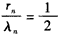 ,得
,得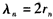 ,
,
同理λn+1=2rn+1,
从而λn+1=λn+rn+rn+1=2rn+1,
将λn=2rn代入,解得rn+1=3rn,
故{rn}为公比q=3的等比数列.
(Ⅱ)由于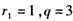 ,
,
故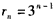 ,从而
,从而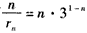 ,
,
即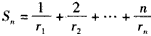 ,
,
则有Sn=1+2×3-1+3×3-2+... +n·31-n, ①
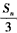 =1×3-1+2×3-2+…+(n-1)·31-n+n·3-n, ②
=1×3-1+2×3-2+…+(n-1)·31-n+n·3-n, ②
①-②,得
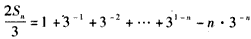
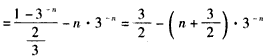 ,
,
∴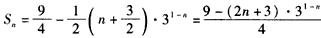 。
。
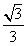 x的倾斜角记为θ,则有
x的倾斜角记为θ,则有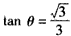 ,
,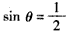 ,
,设Cn的圆心为
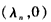 ,
,则由题意知
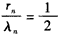 ,得
,得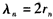 ,
,同理λn+1=2rn+1,
从而λn+1=λn+rn+rn+1=2rn+1,
将λn=2rn代入,解得rn+1=3rn,
故{rn}为公比q=3的等比数列.
(Ⅱ)由于
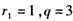 ,
,故
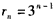 ,从而
,从而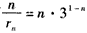 ,
,即
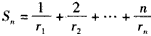 ,
,则有Sn=1+2×3-1+3×3-2+... +n·31-n, ①
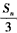 =1×3-1+2×3-2+…+(n-1)·31-n+n·3-n, ②
=1×3-1+2×3-2+…+(n-1)·31-n+n·3-n, ② ①-②,得
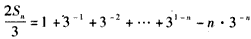
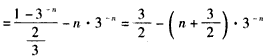 ,
,∴
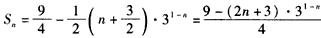 。
。
练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
 如图,椭圆C0:
如图,椭圆C0: