Question

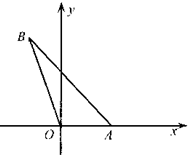（2010•济宁一模）如图，在平面直角坐标系xoy中，点A在x轴的正半轴上，直线AB的倾斜角为

3

4

π，

.

O B

.

=2，设∠AOB=θ，θ∈（

π

2

，

3

4

π）．
（1）用θ表示点B的坐标及|OA|．
（2）若tanθ=-

4

3

，求

OA

•

OB

的值．

Answer 1

分析：（1）由三角函数的定义，可得B的坐标为（2cosθ，2sinθ）．根据三角形内角和定理，结合直线AB的倾斜角等于

3π

4

算出B=

3

4

π-θ，然后在△AOB中利用正弦定理，即可算出用θ表示|OA|的式子；
（2）根据tanθ=-

4

3

，由同角三角三角函数的基本关系算出sinθ、cosθ的值，从而算出sin(

3

4

π-θ)=

2

10

，结合平面向量数量积的公式代入前面的数据，即可得到数量积

OA

•

OB

的值．

解答：解：（1）由三角函数的定义，得点B的坐标为（2cosθ，2sinθ）．…（2分）
∵在△AOB中，∠BAO=

π

4

，∴∠B=π-

π

4

-θ=

3

4

π-θ，
由正弦定得，得

|OB|

sin π 4

=

|OA|

sinB

…（4分）
即

2

2 2

=

|OA|

sin( 3 4 π-θ)

所以|OA|=2

2

sin(

3

4

π-θ)…（6分）
（2）由（1）得

OA

•

OB

=|

OA

|•|

OB

|cosθ=4

2

sin(

3

4

π-θ)•cosθ．…（8分）
∵tanθ=-

4

3

，θ∈(

π

2

，

3

4

π)
∴

sin2θ+cos2θ=1 sinθ cosθ =- 4 3

，解之得sinθ=

4

5

，cosθ=-

3

5

…（10分）
由此可得sin(

3

4

π-θ)=sin

3

4

π•cosθ-cos

3

4

π•sinθ=

2

2

•(-

3

5

)-(-

2

2

)•

4

5

=

2

10

．
∴

OA

•

OB

=4

2

•

2

10

•(-

3

5

)=-

12

25

．…（12分）

点评：本题将三角形放置于坐标系中，在已知直线倾角的情况下求向量的数量积．着重考查了平面向量的数量积公式、同角三角函数的基本关系和利用正弦定理解三角形等知识，属于中档题．