题目内容
过点P（4，2）引圆x2+y2+2x-2y+1=0的切线，则切线长等于（ ）
| A、5 | ||
B、
| ||
C、2
| ||
| D、6 |
分析：把圆的方程化为标准方程后，找出圆心A的坐标和圆的半径r，根据题意画出图形，如图所示，因为PQ为圆A的切线，所以AQ垂直于直线PQ，所以三角形APQ为直角三角形，然后|AQ|为圆A的半径，利用两点间的距离公式求出|AP|的长，利用勾股定理即可求出切线长|PQ|的长．
解答：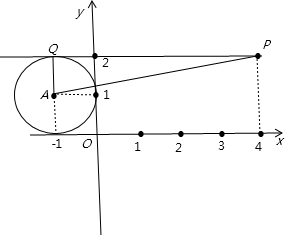
解：把圆的方程化为标准方程得：（x+1）2+（y-1）2=1，
得到圆心A坐标为（-1，1），圆的半径r=1，过点P作圆A的切线PQ，切点为Q，
由|AP|=
=
，|AQ|=r=1，
则切线长|PQ|=
=5．
故选A
解：把圆的方程化为标准方程得：（x+1）2+（y-1）2=1，得到圆心A坐标为（-1，1），圆的半径r=1，过点P作圆A的切线PQ，切点为Q，
由|AP|=
| (4+1)2+(2-1)2 |
| 26 |
则切线长|PQ|=
| |AP|2-|AQ|2 |
故选A
点评：此题考查学生掌握直线与圆相切时所满足的条件，考查了数形结合的数学思想，是一道基础题．
练习册系列答案
相关题目