题目内容
已知函数![]() .
.
(1)解关于![]() 不等式
不等式![]() ;
;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(1)不等式可化为:![]() .
.
当![]() 时,解集为
时,解集为![]()
当![]() 时,解集为
时,解集为![]()
当![]() 时,解集为
时,解集为![]()
(2)由f(x+1)+f(2x)≤![]() +
+![]() 得:
得:
|x+1|+|2x|≤![]() +
+![]() .
.
∵0<a<1,∴0<1-a<1,
∴![]() +
+![]() =
=![]() ≥
≥![]() =4.
=4.
当且仅当a=1-a,即a=![]() 时取“=”.
时取“=”.
∴原问题等价于|x+1|+|2x|≤4,
∴![]() 或
或![]() 或
或![]()
∴-![]() ≤x≤1.
≤x≤1.
∴x的取值范围是{x|-![]() ≤x≤1}.
≤x≤1}.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. ;
; ,且
,且 ,求证:
,求证: .
.
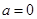 ,解不等式
,解不等式 ;
; 的不等式
的不等式
 .
. ;
; ,若函数
,若函数 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围; 有解,求实数a的取值范围.[来源:]
有解,求实数a的取值范围.[来源:]