题目内容
已知函数 .
.
(1)解不等式 ;
;
(2)若 ,且
,且 ,求证:
,求证: .
.
【答案】
(1)不等式 的解集为
的解集为 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】
试题分析:本题考查解绝对值不等式和证明不等式,意在考查考生运用函数零点分类讨论的解题思想.第一问,利用函数零点将绝对值去掉,将函数转化为分段函数,分类讨论解不等式;第二问,先利用已知函数将所证结论进行转化变成 ,再利用作差法先证
,再利用作差法先证 ,再开方即可.
,再开方即可.
试题解析:(Ⅰ) ,
,
当 时,由
时,由 ,解得
,解得 ;
;
当 时,
时, 不成立;
不成立;
当 时,由
时,由 ,解得
,解得 .
…4分
.
…4分
所以不等式 的解集为
的解集为 .
…5分
.
…5分
(Ⅱ) 即
即 .
…6分
.
…6分
因为 ,
,
所以 ,
,
所以 .
.
故所证不等式成立. …10分
考点:1.解绝对值不等式;2.作差法证明不等式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.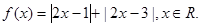 .
.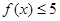 ;
;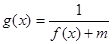 的定义域为
的定义域为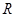 ,求实数
,求实数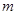 的取值范围.
的取值范围.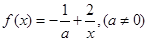 ,
,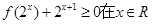 上恒成立,求a的取值范围。
上恒成立,求a的取值范围。  .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围. .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.