题目内容
函数 为定义在
为定义在 上的减函数,函数
上的减函数,函数 的图像关于点(1,0)对称,
的图像关于点(1,0)对称,  满足不等式
满足不等式 ,
, ,
, 为坐标原点,则当
为坐标原点,则当 时,
时, 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
D
解析试题分析:因为函数 的图像关于点(1,0)对称,所以函数
的图像关于点(1,0)对称,所以函数 的图像关于原点对称,即
的图像关于原点对称,即 是奇函数。又因为
是奇函数。又因为 为定义在
为定义在 上的减函数,所以由
上的减函数,所以由 ,所以
,所以 ,令
,令 ,由线性规划的知识可知
,由线性规划的知识可知 的取值范围为
的取值范围为 。
。
考点:函数的单调性;函数的奇偶性;图像的变换;向量的数量积;线性规划的有关知识。
点评:把抽象函数的问题和线性规划的有关知识相结合,难度较大。对学生的能力要求较高。

练习册系列答案
相关题目
下列函数是偶函数的是( )
A.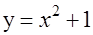 , ,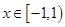 | B.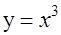 |
C. | D. |
函数 的定义域为 ( )
的定义域为 ( )
| A.(e,+∞) | B.[e,+∞) | C. (O,e] | D.(-∞,e] |
下面各组函数中是同一函数的是 ( )
A. |
B. 与 与 |
C. |
D. |
已知函数 的定义域为M,
的定义域为M, 的定义域为N,则M
的定义域为N,则M
 =
=
A.{ } } | B.{ } } |
C. | D.( }) }) |
下列函数中,最小值为4的是 ( )
A. | B. |
C. | D. |
若函数 ( )
( )
A. | B. | C.15 | D. |
已知函数 的值域为
的值域为 ,则( )
,则( )
A. | B. | C. | D. |
 的定义域为
的定义域为 ,值域为
,值域为 ,则点
,则点 表示的图形可以是( )
表示的图形可以是( ) 