题目内容
定义在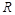 上的函数
上的函数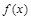 的图象关于点
的图象关于点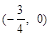 成中心对称,对任意的实数
成中心对称,对任意的实数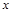 都有
都有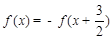 ,且
,且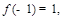
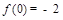 ,则
,则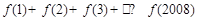 的值为
的值为
( )
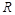 上的函数
上的函数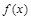 的图象关于点
的图象关于点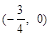 成中心对称,对任意的实数
成中心对称,对任意的实数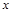 都有
都有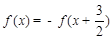 ,且
,且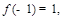
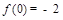 ,则
,则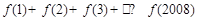 的值为
的值为( )
A.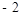 | B.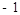 | C.0 | D.1 |
D
分析:先根据条件确定函数的周期,再由函数的图象关于点(- ,0)成中心对称知为奇函数,从而求出f(1)、f(2)、f(3)的值,最终得到答案.
,0)成中心对称知为奇函数,从而求出f(1)、f(2)、f(3)的值,最终得到答案.
解答:解:由f(x)=-f(x+ )得f(x)=f(x+3)即周期为3,
)得f(x)=f(x+3)即周期为3,
由图象关于点(- ,0)成中心对称得f(x)+f(-x-
,0)成中心对称得f(x)+f(-x- )=0,
)=0,
从而-f(x+ )=-f(-x-
)=-f(-x- ),所以f(x)=f(-x).
),所以f(x)=f(-x).
由f(-1)=1,f(0)=-2,
∴f(1)=f(4)=…=f(2008)=1,
f(2)=f(5)=…=f(2006)=1,
f(3)=f(6)=…=f(2007)=-2,
∴f(1)+f(2)+f(3)+…+f(2008)+…+f(2008)=f(1)=1
故选D
 ,0)成中心对称知为奇函数,从而求出f(1)、f(2)、f(3)的值,最终得到答案.
,0)成中心对称知为奇函数,从而求出f(1)、f(2)、f(3)的值,最终得到答案.解答:解:由f(x)=-f(x+
 )得f(x)=f(x+3)即周期为3,
)得f(x)=f(x+3)即周期为3,由图象关于点(-
 ,0)成中心对称得f(x)+f(-x-
,0)成中心对称得f(x)+f(-x- )=0,
)=0,从而-f(x+
 )=-f(-x-
)=-f(-x- ),所以f(x)=f(-x).
),所以f(x)=f(-x).由f(-1)=1,f(0)=-2,
∴f(1)=f(4)=…=f(2008)=1,
f(2)=f(5)=…=f(2006)=1,
f(3)=f(6)=…=f(2007)=-2,
∴f(1)+f(2)+f(3)+…+f(2008)+…+f(2008)=f(1)=1
故选D

练习册系列答案
相关题目
 在
在 处连续,则
处连续,则


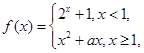 若
若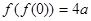 ,则实数
,则实数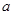 等于
等于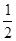
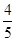
 上的奇函数和偶函数,当x <0时,
上的奇函数和偶函数,当x <0时, ,且g(-3)=0,则不等式f(x)g(x)<0的解集是 ( )
,且g(-3)=0,则不等式f(x)g(x)<0的解集是 ( )



 =
= 的图象的对称中心为点(1,1).
的图象的对称中心为点(1,1). 的值;
的值;  =
= (
( <2
<2 ,求实数
,求实数 的取值范围.
的取值范围. ,若
,若 且
且 .
. .
. 那么不等式
那么不等式 的解集为 。
的解集为 。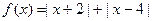 的最小值是 。
的最小值是 。 上连续不断,定义:
上连续不断,定义: ,
, ,其中,
,其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 对任意的
对任意的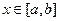 成立,则称函数
成立,则称函数 上的“
上的“ 阶收缩函数” .
阶收缩函数” . 为[-1,4]上的“
为[-1,4]上的“