题目内容
设f(x)=
,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2014(x)= .
| 1+x |
| 1-x |
考点:数列递推式,数列的函数特性
专题:等差数列与等比数列
分析:由于f(x)=
,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,可得f5(x)=f(f4(x))=
=f(x)=f1(x).于是f2014(x)=f503×4+2(x)=f2(x).即可得出.
| 1+x |
| 1-x |
| 1+x |
| 1-x |
解答:
解:∵f(x)=
,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,
∴f2(x)=f(f1(x))=
=
=-
,f3(x)=f(f2(x))=
=
,f4(x)=f(f3(x))=
=
=x,f5(x)=f(f4(x))=
=f(x)=f1(x).
∴fn+4(x)=fn(x).
∴f2014(x)=f503×4+2(x)=f2(x)=-
.
故答案为:-
.
| 1+x |
| 1-x |
∴f2(x)=f(f1(x))=
1+
| ||
1-
|
| 2 |
| -2x |
| 1 |
| x |
1-
| ||
1+
|
| x-1 |
| x+1 |
1+
| ||
1-
|
| 2x |
| 2 |
| 1+x |
| 1-x |
∴fn+4(x)=fn(x).
∴f2014(x)=f503×4+2(x)=f2(x)=-
| 1 |
| x |
故答案为:-
| 1 |
| x |
点评:本题考查了数列与函数的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知正实数a,b满足a+2b=1,则
的最小值为( )
| b+a |
| ab |
A、3+2
| ||
B、1+
| ||
| C、4 | ||
D、2
|
设a,b,c为正数,a+b+9c2=1,则
+
+
c的最大值是( )
| a |
| b |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
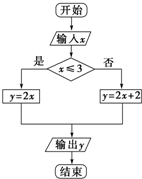 根据如图的框图回答后面的问题.
根据如图的框图回答后面的问题.