题目内容
已知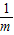 +
+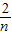 =1(m>0,n>0),当mn取得最小值时,直线y=-
=1(m>0,n>0),当mn取得最小值时,直线y=-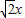 +2与曲线
+2与曲线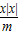 +
+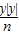 =1的交点的个数为( )
=1的交点的个数为( )A.1
B.2
C.3
D.4
【答案】分析:由基本不等式可得mn的值,由分类讨论去掉绝对值可得曲线,作出两个图象可得答案.
解答: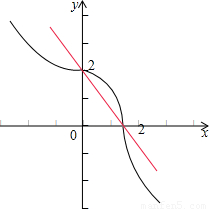 解:∵1=
解:∵1=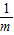 +
+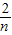 ≥2
≥2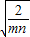 ,∴
,∴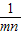 ≤
≤ ,mn≥8,
,mn≥8,
当且仅当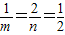 ,即m=2,n=4时,mn取得最小值8,
,即m=2,n=4时,mn取得最小值8,
故曲线方程为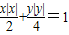 ,
,
当x≥0,y≥0时,方程化为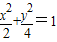
当x<0,y>0时,方程化为-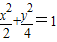 ,
,
当x>0,y<0时,方程化为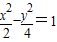 ,
,
当x<0,y<0时,无意义,
由圆锥曲线可作出方程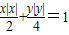 和直线y=-
和直线y=-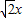 +2与的图象,
+2与的图象,
由图象可知,交点的个数为2,
故选B
点评:本题考查根的存在性及判断,涉及基本不等式和圆锥曲线的知识,属中档题.
解答:
 解:∵1=
解:∵1=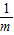 +
+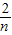 ≥2
≥2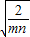 ,∴
,∴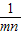 ≤
≤ ,mn≥8,
,mn≥8,当且仅当
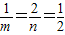 ,即m=2,n=4时,mn取得最小值8,
,即m=2,n=4时,mn取得最小值8,故曲线方程为
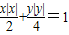 ,
,当x≥0,y≥0时,方程化为
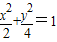
当x<0,y>0时,方程化为-
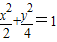 ,
,当x>0,y<0时,方程化为
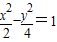 ,
,当x<0,y<0时,无意义,
由圆锥曲线可作出方程
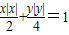 和直线y=-
和直线y=-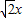 +2与的图象,
+2与的图象,由图象可知,交点的个数为2,
故选B
点评:本题考查根的存在性及判断,涉及基本不等式和圆锥曲线的知识,属中档题.

练习册系列答案
相关题目
 +
+ =1(m>0,n>0),当mn取得最小值时,直线y=-
=1(m>0,n>0),当mn取得最小值时,直线y=- +2与曲线
+2与曲线 +
+ =1的交点的个数为
=1的交点的个数为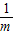 +
+ =1(m>0,n>0),当mn取得最小值时,直线y=-
=1(m>0,n>0),当mn取得最小值时,直线y=-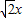 +2与曲线
+2与曲线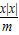 +
+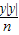 =1的交点的个数为( )
=1的交点的个数为( )