题目内容
如图13,已知AB为半圆O的直径,AP为过点A的半圆的切线,在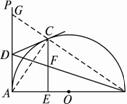
(1) (2)
图13
(1)当点C为![]() 的中点时(如图13(1)),求证:CF =EF;
的中点时(如图13(1)),求证:CF =EF;
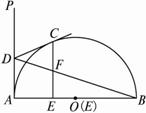
(2)当点C不是![]() 的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
思路分析:第(1)题E与O重合,只需证明四边形DAEC为矩形,CD∥AB即可.?
(2)由(1)的结论猜测CF =EF仍然成立.然后再设法证明.
证明:(1)∵DA是切线,AB为直径,∴DA⊥AB.?
∵点C是![]() 的中点,且CE⊥AB,?
的中点,且CE⊥AB,?
∴CE过圆心.∴点E为半圆的圆心.?
又∵DC是切线,∴DC⊥EC.?
∴四边形DAEC为矩形.?
∴CE∥AD且CE =AD.?
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,?
,?
∴F为EC的中点,即CF =EF.?

(2)CF =EF仍然成立.证明如下:?
连结BC并延长交AP于G点,连结AC.?
∵AD、CD是半圆的切线,?
∴DC=DA.∴∠DAC=∠DCA.?
∵AB为直径,?
∴∠ACB =90°,∠ACG =90°,∠G+∠DAC =∠DCA +∠DCG =90°.?
∴∠G = ∠DCG.?
在△GDC中,GD =DC,又∵DC =DA,∴GD =DA.?
∵AP是半圆O的切线,?
∴AP⊥AB.又CE⊥AB,∴CE∥AP.?
∴![]() =
=![]() =
=![]() .?
.?
又GD =AD,∴CF =EF.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
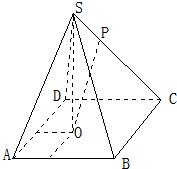 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2和1. P是SC上的点,
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2和1. P是SC上的点,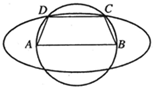 如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为
如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆