题目内容
(本小题满分12分)在平面直角坐标系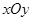 中,已知点
中,已知点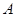
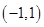 ,P是动点,且三角形
,P是动点,且三角形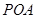 的三边所在直线的斜率满足
的三边所在直线的斜率满足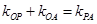 .
.
(Ⅰ)求点P的轨迹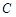 的方程;
的方程;
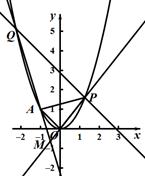
(Ⅱ)若Q是轨迹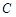 上异于点
上异于点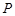 的一个点,且
的一个点,且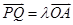 ,直线
,直线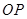 与
与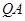 交于点M,试探
交于点M,试探
究:点M的横坐标是否为定值?并说明理由.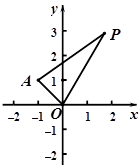
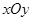 中,已知点
中,已知点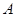
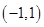 ,P是动点,且三角形
,P是动点,且三角形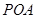 的三边所在直线的斜率满足
的三边所在直线的斜率满足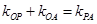 .
.(Ⅰ)求点P的轨迹
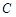 的方程;
的方程;(Ⅱ)若Q是轨迹
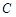 上异于点
上异于点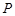 的一个点,且
的一个点,且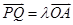 ,直线
,直线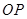 与
与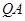 交于点M,试探
交于点M,试探究:点M的横坐标是否为定值?并说明理由.

(1)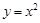 (
(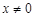 且
且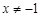 );(2)点M的横坐标为定值
);(2)点M的横坐标为定值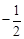 .
.
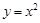 (
(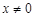 且
且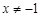 );(2)点M的横坐标为定值
);(2)点M的横坐标为定值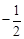 .
.第一问利用已知的斜率关系式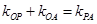 ,设点的坐标代入即可得到轨迹方程。
,设点的坐标代入即可得到轨迹方程。
第二问中,由由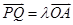 可知直线
可知直线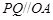 ,则
,则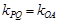 ,然后设出点P,Q的坐标,然后表示一个关系式,然后利用由
,然后设出点P,Q的坐标,然后表示一个关系式,然后利用由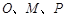 三点共线可知,同理得到关系式,联立解得。
三点共线可知,同理得到关系式,联立解得。
解:(Ⅰ)设点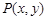 为所求轨迹上的任意一点,则由
为所求轨迹上的任意一点,则由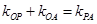 得
得
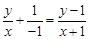 , …………2分
, …………2分
整理得轨迹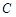 的方程为
的方程为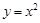 (
(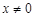 且
且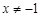 ), …………4分
), …………4分
(Ⅱ)设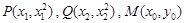 ,
,
由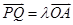 可知直线
可知直线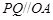 ,则
,则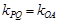 ,
,
故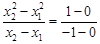 ,即
,即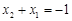 , …………6分
, …………6分
由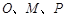 三点共线可知,
三点共线可知,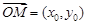 与
与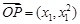 共线,
共线,
∴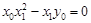 ,
,
由(Ⅰ)知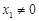 ,故
,故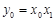 , …………8分
, …………8分
同理,由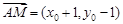 与
与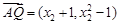 共线,
共线,
∴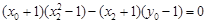 ,即
,即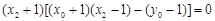 ,
,
由(Ⅰ)知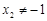 ,故
,故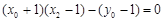 , …………10分
, …………10分
将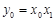 ,
,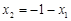 代入上式得
代入上式得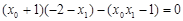 ,
,
整理得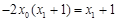 ,
,
由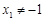 得
得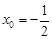 ,即点M的横坐标为定值
,即点M的横坐标为定值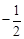 . ………………………12分
. ………………………12分
(方法二)
设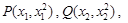
由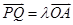 可知直线
可知直线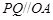 ,则
,则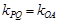 ,
,
故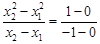 ,即
,即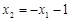 , …………6分
, …………6分
∴直线OP方程为: ①; …………8分
①; …………8分
直线QA的斜率为: ,
,
∴直线QA方程为: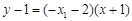 ,即
,即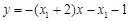 ②;……10分
②;……10分
联立①②,得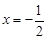 ,∴点M的横坐标为定值
,∴点M的横坐标为定值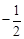 . ………………………12分
. ………………………12分
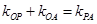 ,设点的坐标代入即可得到轨迹方程。
,设点的坐标代入即可得到轨迹方程。第二问中,由由
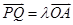 可知直线
可知直线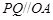 ,则
,则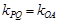 ,然后设出点P,Q的坐标,然后表示一个关系式,然后利用由
,然后设出点P,Q的坐标,然后表示一个关系式,然后利用由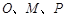 三点共线可知,同理得到关系式,联立解得。
三点共线可知,同理得到关系式,联立解得。解:(Ⅰ)设点
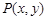 为所求轨迹上的任意一点,则由
为所求轨迹上的任意一点,则由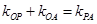 得
得
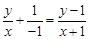 , …………2分
, …………2分整理得轨迹
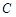 的方程为
的方程为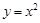 (
(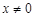 且
且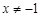 ), …………4分
), …………4分(Ⅱ)设
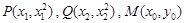 ,
,由
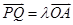 可知直线
可知直线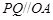 ,则
,则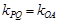 ,
,故
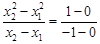 ,即
,即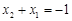 , …………6分
, …………6分由
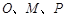 三点共线可知,
三点共线可知,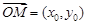 与
与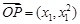 共线,
共线,∴
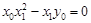 ,
,由(Ⅰ)知
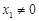 ,故
,故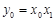 , …………8分
, …………8分同理,由
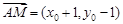 与
与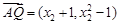 共线,
共线,∴
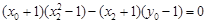 ,即
,即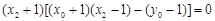 ,
,由(Ⅰ)知
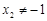 ,故
,故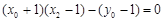 , …………10分
, …………10分将
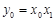 ,
,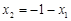 代入上式得
代入上式得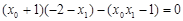 ,
,整理得
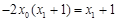 ,
,由
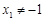 得
得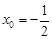 ,即点M的横坐标为定值
,即点M的横坐标为定值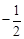 . ………………………12分
. ………………………12分(方法二)
设
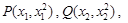
由
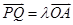 可知直线
可知直线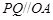 ,则
,则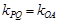 ,
,故
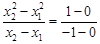 ,即
,即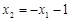 , …………6分
, …………6分∴直线OP方程为:
 ①; …………8分
①; …………8分直线QA的斜率为:
 ,
, ∴直线QA方程为:
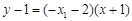 ,即
,即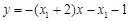 ②;……10分
②;……10分联立①②,得
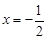 ,∴点M的横坐标为定值
,∴点M的横坐标为定值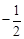 . ………………………12分
. ………………………12分
练习册系列答案
相关题目
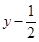 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.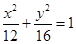 有公共焦点,且离心率互为倒数的双曲线的方程是
有公共焦点,且离心率互为倒数的双曲线的方程是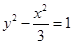
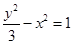

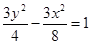
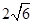 ).
).
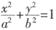 (a>b>0)的两个焦点,若椭圆上存在一点P使得
(a>b>0)的两个焦点,若椭圆上存在一点P使得 ,则椭圆的离心率e的取值范围为________.
,则椭圆的离心率e的取值范围为________. 的焦点在
的焦点在 轴上,左、右顶点分别为
轴上,左、右顶点分别为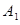 、
、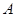 ,上顶点为
,上顶点为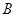 ,抛物线
,抛物线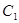 、
、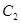 分别以
分别以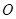 ,
,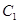 与
与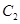 相交于直线
相交于直线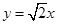 上一点
上一点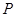 .
.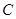 及抛物线
及抛物线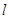 与直线
与直线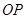 垂直,且与椭圆
垂直,且与椭圆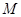 、
、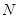 ,已知点
,已知点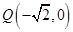 ,求
,求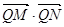 的最小值.
的最小值. 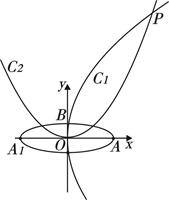
 :
: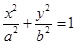
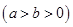 ,称圆心在坐标原点
,称圆心在坐标原点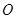 ,半径为
,半径为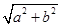 的圆是椭圆
的圆是椭圆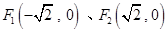 ,椭圆
,椭圆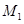 满足
满足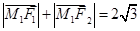 .
.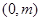
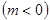 作直线
作直线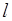 ,使得直线
,使得直线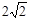 .求出
.求出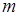 的值.
的值.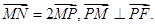
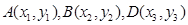 是曲线C上的点,且
是曲线C上的点,且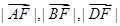 成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。 ABC内(含边界)一动点,且到三个侧面PAB,PBC,PCA的距离成等差数列,则点M的轨迹是( )
ABC内(含边界)一动点,且到三个侧面PAB,PBC,PCA的距离成等差数列,则点M的轨迹是( )