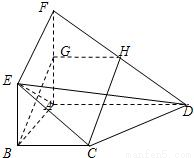
题目内容
如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
AD,BE
AF,G、H分别是FA、FD的中点.
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?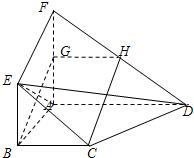
| ||
| . |
| 1 |
| 2 |
| ||
| . |
| 1 |
| 2 |
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?


证明:(Ⅰ)由题意知,FG=GA,FH=HD
所以GH
| ||
| . |
| 1 |
| 2 |
| ||
| . |
| 1 |
| 2 |
| ||
| . |
所以四边形BCHG是平行四边形.
(Ⅱ)C,D,F,E四点共面.理由如下:
由BE
| ||
| . |
| 1 |
| 2 |
| ||
| . |
| ||
| . |
所以EF∥BG
由(Ⅰ)知BG∥CH,所以EF∥CH,故EC,FH共面.
又点D在直线FH上
所以C,D,F,E四点共面.

练习册系列答案
相关题目
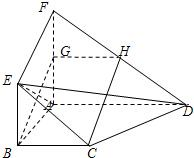 如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
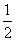 AD,BE
AD,BE
 AF,G、H分别是FA、FD的中点,
AF,G、H分别是FA、FD的中点,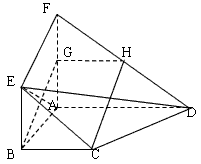

 AD,BE
AD,BE
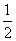 AF.
AF.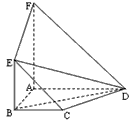
 AD,BE
AD,BE
 AF,G、H分别是FA、FD的中点.
AF,G、H分别是FA、FD的中点.