题目内容
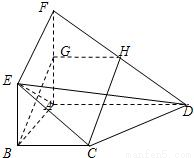
如图，面ABEF⊥面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠BAF=90°，BC
AD，BE
AF．
（Ⅰ）求证：C、D、E、F四点共面；
（Ⅱ）若BA=BC=BE，求二面角A-ED-B的大小．
AD，BEAF．（Ⅰ）求证：C、D、E、F四点共面；
（Ⅱ）若BA=BC=BE，求二面角A-ED-B的大小．
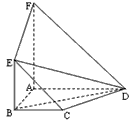
（Ⅰ）证明：∵面ABEF⊥面ABCD，AF⊥AB，
∴AF⊥面ABCD，
∴以A为原点，以AB，AD，AF所在直线为x轴，y轴，z轴，建立如图所示的空间直角坐标系A-xyz，
不妨设AB=a，AD=2b，AF=2c，
则
，
∴
，
，
∴
，∴
，
∵
，
∴DF∥CE，
∴C、D、E、F四点共面．
（Ⅱ）解：设AB=1，则BC=BE=1，
∴
，
设平面AED的法向量为
，
由
，得
，
，
设平面BED的法向量为
，
由
，得
，
，
，
由图知，二面角A-ED-B为锐角，
∴其大小为
．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
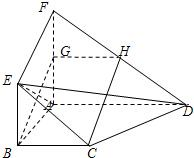如图，面ABEF⊥面ABCD，四边形ABEF与四边形ABCD都是直角梯形，∠BAD=∠FAB=90°，BC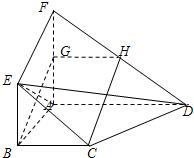
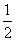AD，BE
AF，G、H分别是FA、FD的中点，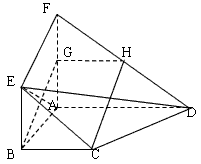
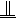
AD，BE
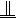
AF，G、H分别是FA、FD的中点．