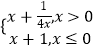Question

【题目】已知函数 有最大值 ， ，且 是 的导数．
（Ⅰ）求 的值；
（Ⅱ）证明：当 ， 时， ．

Answer 1

【答案】解：（Ⅰ） 的定义域为 ， ．
当 时， ，
在 上为单调递增函数，无最大值，不合题意，舍去；
当 时，令 ，得 ，
当 时， ，函数 单调递增；
当 时， ，函数 单调递减，
,
,
．
（Ⅱ）由（Ⅰ）可知， ,
．
， ,
在 上单调递增．
又 ， 且 ,
．
,
当 时， ， 单调递增,
要证 ，即 ，只要证 ，即 ．
， ,
所以只要证 ————（*）,
设 （其中 ）,
,
在（0，1）上为增函数,
，故（*）式成立，从而
【解析】（Ⅰ）根据题目中所给的条件的特点，求出函数的导数，通过讨论a的范围，利用导数和函数的单调性的关系求出函数的单调区间；
（Ⅱ）求出函数的导数，根据函数的单调性问题进行等价转化为函数的最值问题求解即可.主要考查导数的几何意义、导数及其应用、不等式等基础知识.
【考点精析】利用利用导数研究函数的单调性和函数的极值对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；极值反映的是函数在某一点附近的大小情况．