题目内容
已知函数
，其中常数a > 0．
(1) 当a = 4时，证明函数f(x)在
上是减函数；
(2) 求函数f(x)的最小值．
解：(1) 当
时，
，…………………………………………1分
任取0<x1<x2≤2，则f(x1)–f(x2)=
………………3分
因为0<x1<x2≤2，所以f(x1)–f(x2)>0，即f(x1)>f(x2)………………………………………5分
所以函数f(x)在上是减函数；………………………………………………………6分
(2)
，……………………………………………………7分
当且仅当
时等号成立，…………………………………………………………8分
当
，即
时，
的最小值为
，………………………10分
当
，即
时，在上单调递减，…………………………………11分
所以当
时，取得最小值为
，………………………………………………13分
综上所述：
………………………………………14分
练习册系列答案
相关题目
（其中常数a，b∈R），
．
时，求函数g（x）在[0，a]上的最小值h（a），并探索：是否存在满足条件的实数a，使得对任意的x∈R，f（x）＞h（a）恒成立．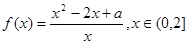
，其中常数a > 0．
上是减函数；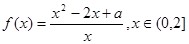
，其中常数a > 0．
上是减函数；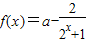
（其中常数a∈R）
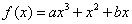（其中常数a,b∈R）,
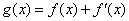是奇函数.
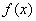的表达式;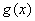
的单调性，并求