题目内容
已知函数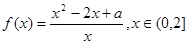 ,其中常数a > 0.
,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在 上是减函数;
上是减函数;
(2) 求函数f(x)的最小值.
【答案】
解:(1) 当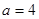 时,
时,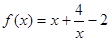 ,利用“定义法”证明。
,利用“定义法”证明。
(2) 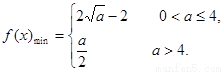
【解析】
试题分析:
思路分析:(1) 当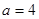 时,
时,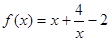 ,利用“定义法”证明。执行“设、算、证、结”。
,利用“定义法”证明。执行“设、算、证、结”。
(2)应用均值定理及“对号函数”的单调性,分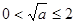 ,即
,即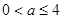 和
和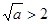 ,即
,即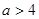 两种情况讨论得到:
两种情况讨论得到: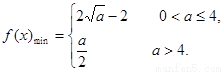 。
。
解:(1) 当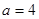 时,
时,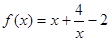 ,
,
任取0<x1<x2≤2,则f(x1)–f(x2)=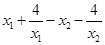
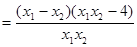
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2)
所以函数f(x)在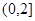 上是减函数;
上是减函数;
(2)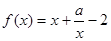
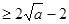 ,当且仅当
,当且仅当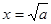 时等号成立,
时等号成立,
当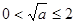 ,即
,即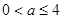 时,
时,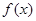 的最小值为
的最小值为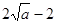 ,
,
当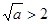 ,即
,即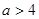 时,
时,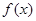 在
在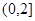 上单调递减,
上单调递减,
所以当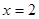 时,
时,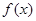 取得最小值为
取得最小值为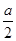 ,
,
综上所述: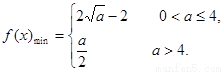
考点:函数的单调性,“对号函数的性质”,均值定理的应用。
点评:中档题,本题综合性较强,研究函数的单调性,可以利用导数,也可以利用常见函数的单调性。应用均值定理,要注意“一正,二定,三相等”。

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 (其中常数a,b∈R),
(其中常数a,b∈R), .
. 时,求函数g(x)在[0,a]上的最小值h(a),并探索:是否存在满足条件的实数a,使得对任意的x∈R,f(x)>h(a)恒成立.
时,求函数g(x)在[0,a]上的最小值h(a),并探索:是否存在满足条件的实数a,使得对任意的x∈R,f(x)>h(a)恒成立.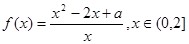 ,其中常数a > 0.
,其中常数a > 0.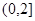 上是减函数;
上是减函数;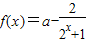 (其中常数a∈R)
(其中常数a∈R)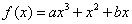 (其中常数a,b∈R),
(其中常数a,b∈R),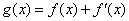 是奇函数.
是奇函数.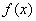 的表达式;
的表达式;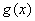 的单调性,并求
的单调性,并求