题目内容
(本小题满分14分)设数列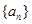 是首项为0的递增数列,
是首项为0的递增数列,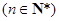 ,
,
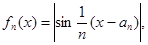
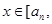
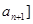 满足:对于任意的
满足:对于任意的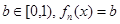 总有两个不同的根. (Ⅰ)试写出
总有两个不同的根. (Ⅰ)试写出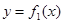 ,并求出
,并求出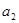 ;
;
(Ⅱ)求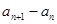 ,并求出
,并求出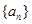 的通项公式;
的通项公式;
(Ⅲ)设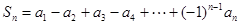 ,求
,求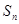 .
.
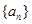 是首项为0的递增数列,
是首项为0的递增数列,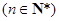 ,
,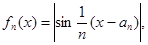
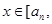
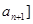 满足:对于任意的
满足:对于任意的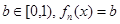 总有两个不同的根. (Ⅰ)试写出
总有两个不同的根. (Ⅰ)试写出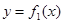 ,并求出
,并求出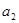 ;
; (Ⅱ)求
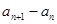 ,并求出
,并求出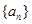 的通项公式;
的通项公式;(Ⅲ)设
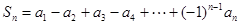 ,求
,求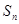 .
.(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)∴
;(Ⅲ)∴ .
.
 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)∴
;(Ⅲ)∴ .
.(1)∵ ,当
,当 时,
时, ,
, . 又∵对任意的
. 又∵对任意的 ,
, 总有两个不同的根,∴
总有两个不同的根,∴ .
.
(2) 类比(Ⅰ)中a2的求法,可知 ,
, ,从而归纳出
,从而归纳出 ,
,  .
.
(3) 分两种情况: ,和
,和 ,分别求解.
,分别求解.
解:(Ⅰ)∵ ,当
,当 时,
时, ,
, ,
,
又∵对任意的 ,
, 总有两个不同的根,∴
总有两个不同的根,∴
∴ ,
, 
(Ⅱ)由(Ⅰ),
∵对任意的 ,
, 总有两个不同的根, ∴
总有两个不同的根, ∴

∵对任意的 ,
, 总有两个不同的根, ∴
总有两个不同的根, ∴
由此可得 ,
, 
(Ⅲ)当 ,
,

∴
当 ,
,
∴
 ,当
,当 时,
时, ,
, . 又∵对任意的
. 又∵对任意的 ,
, 总有两个不同的根,∴
总有两个不同的根,∴ .
.(2) 类比(Ⅰ)中a2的求法,可知
 ,
, ,从而归纳出
,从而归纳出 ,
,  .
.(3) 分两种情况:
 ,和
,和 ,分别求解.
,分别求解.解:(Ⅰ)∵
 ,当
,当 时,
时, ,
, ,
, 又∵对任意的
 ,
, 总有两个不同的根,∴
总有两个不同的根,∴
∴
 ,
, 
(Ⅱ)由(Ⅰ),

∵对任意的
 ,
, 总有两个不同的根, ∴
总有两个不同的根, ∴

∵对任意的
 ,
, 总有两个不同的根, ∴
总有两个不同的根, ∴
由此可得
 ,
, 
(Ⅲ)当
 ,
,

∴

当
 ,
,
∴


练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
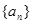 的前项和为
的前项和为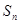 ,已知
,已知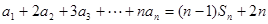 (
(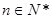 ).
).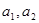 的值;
的值;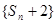 是等比数列;
是等比数列;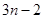 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列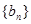 ,若
,若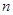 项的和为
项的和为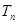 ,求证:
,求证: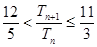 .
.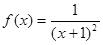 ,数列
,数列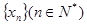 的项满足:
的项满足: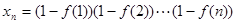 ,(1)试求
,(1)试求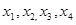
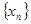 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.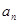 }中,
}中,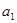 =1,
=1,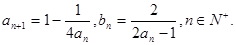 (1)求
(1)求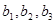
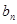 }的通项公式(不要求证明);(2)求证:对于任意的n
}的通项公式(不要求证明);(2)求证:对于任意的n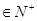 都有
都有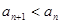 ;(3)设
;(3)设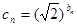 证明:数列{
证明:数列{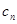 }不存在成等差数列的三项。
}不存在成等差数列的三项。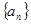 满足
满足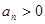 且对一切
且对一切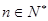 ,
,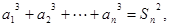
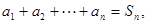
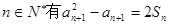
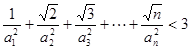
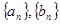 满足:
满足: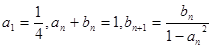
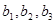 的值; 2)求证数列
的值; 2)求证数列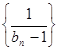 是等差数列,并求数列
是等差数列,并求数列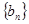 的通项公式;
的通项公式;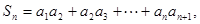 若
若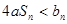 恒成立,求实数
恒成立,求实数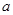 的取值范围.
的取值范围.
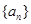 为等差数列,且
为等差数列,且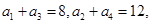 (Ⅰ)求数列
(Ⅰ)求数列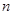 项和为
项和为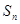 ,若
,若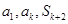 成等比数列,求正整数
成等比数列,求正整数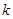 的值。
的值。 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 、
、 、
、 成等比数列。
成等比数列。 ,求数列
,求数列 的前
的前 项和
项和 。
。 满足:
满足: ,且
,且 的取值范围是( )
的取值范围是( )


