题目内容
14.设a=$\frac{1}{lo{g}_{4}3}$+$\frac{1}{lo{g}_{7}3}$,且a∈(k,k+1),k∈z,则k=3.分析 根据换底公式的推论,logab•logba=1,将已知中的对数式化为底数为3的对数式,再由对数的运算性质,得到答案.
解答 解:a=$\frac{1}{lo{g}_{4}3}$+$\frac{1}{lo{g}_{7}3}$=log34+log37=log328∈(3,4),
故k=3,
故答案为:3
点评 本题考查的知识点是对数的运算性质,熟练掌握对数的运算性质,是解答的关键.

练习册系列答案
相关题目
5.函数f(x)=xex+a在R上取得最小值1-$\frac{1}{e}$,则函数g(x)=$\frac{f(x)}{{e}^{x}}$在区间(-∞,0)上一定( )
| A. | 有最小值 | B. | 有最大值 | C. | 是减函数 | D. | 是增函数 |
6.下列说法错误的是( )
| A. | 一个算法应包含有限的操作步骤,而不能是无限的 | |
| B. | 有的算法执行完后,可能有无数个结果 | |
| C. | 一个算法可以有0个或多个输入 | |
| D. | 算法中的每一步都是确定的,算法的含义是唯一的 |
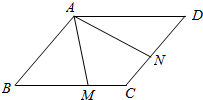 如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.
如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.