题目内容
1.函数f(x)是定义在R上偶函数,当x≥0时,f(x)单调递减.则下列各式成立的是( )| A. | f(1)<f(-3) | B. | f(3)>f(2) | C. | f(-2)>f(3) | D. | f(2)>f(0) |
分析 利用函数f(x)是定义在R上偶函数,当x≥0时,f(x)单调递减,即可比较大小.
解答 解:∵f(x)是R上的偶函数,∴f(-2)=f(2),
又∵f(x)在[0,+∞)上递减,
∴f(-2)>f(3).
故选:C.
点评 本题主要考查大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知圆(x-a)2+(y-b)2=1与两直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,则$\frac{b}{a+2}$的取值范围为( )
| A. | [-$\frac{1}{2}$,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,$\frac{3}{4}$] | C. | (-∞,-$\frac{1}{2}$]∪[$\frac{3}{4}$,+∞) | D. | [-$\frac{21}{22}$,$\frac{14}{27}$] |
9.要得到函数y=sin(x+$\frac{π}{6}$)的图象,只需要将函数y=cosx的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
16.设抛物线y2=4x的焦点为F,过F作倾角为60°的直线交抛物线于A、B两点(点A在第一象限),与其准线交于点C,则$\frac{{S}_{△AOC}}{{S}_{BOF}}$=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
6.已知函数f(x-1)的定义域是(1,2),那么f(2x)的定义域是( )
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | (-∞,0) | D. | (0,+∞) |
10.三个数0.42,20.4,log0.42的大小关系为( )
| A. | 0.42<20.4<log0.42 | B. | log0.42<0.42<20.4 | ||
| C. | 0.42<log0.42<20.4 | D. | log0.42<20.4<0.42 |
11.下列各组函数表示同一个函数的是( )
| A. | $f(x)=\frac{{{x^2}-1}}{x-1}$,g(x)=x+1 | B. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ | ||
| C. | $f(x)={({\sqrt{x-1}})^2}$,g(x)=|x-1| | D. | f(x)=2x-1,g(t)=2t-1 |
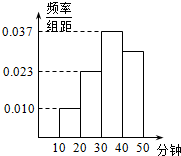 某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在40~50分钟的人数为81.
某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在40~50分钟的人数为81.