题目内容
12.已知圆(x-a)2+(y-b)2=1与两直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,则$\frac{b}{a+2}$的取值范围为( )| A. | [-$\frac{1}{2}$,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,$\frac{3}{4}$] | C. | (-∞,-$\frac{1}{2}$]∪[$\frac{3}{4}$,+∞) | D. | [-$\frac{21}{22}$,$\frac{14}{27}$] |
分析 圆(x-a)2+(y-b)2=1与二直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,可得圆心C到直线的距离小于等于半径,即可求$\frac{b}{a+2}$的取值范围.
解答 解:∵圆:(x-a)2+(y-b)2=1,圆心为C(a,b),半径为1.
∵直线l1:3x-4y-1=0和圆:(x-a)2+(y-b)2=1有公共点,
∴圆心C到直线的距离:$\frac{|3a-4b-1|}{5}$≤1,即$\left\{\begin{array}{l}{3a-4b-6≤0}\\{3a-4b+4≥0}\end{array}\right.$…①
∵直线l2:4x+3y+1=0和圆:(x-a)2+(y-b)2=1有公共点,
∴圆心C到直线的距离:$\frac{|4a+3b+1|}{5}$≤1,即$\left\{\begin{array}{l}{4a+3b-4≤0}\\{4a-3b+6≥0}\end{array}\right.$…②
∴作出①②不等式组表示的平面区域如图: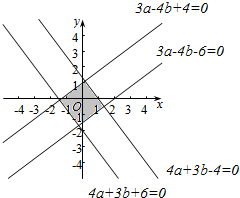
∴由$\left\{\begin{array}{l}{3a-4b+4=0}\\{4a+3b-4=0}\end{array}\right.$得B($\frac{4}{25}$,$\frac{28}{25}$).E(-2,0).
由$\left\{\begin{array}{l}{3a-4b-6=0}\\{4a+3b+6=0}\end{array}\right.$得D(-$\frac{6}{25}$,-$\frac{42}{25}$)
∴由$\frac{b}{a+2}$的几何意义可得,最大值为kBE=$\frac{14}{27}$,最小值为kED=-$\frac{21}{22}$,
∴$\frac{b}{a+2}$的取值范围为[-$\frac{21}{22}$,$\frac{14}{27}$],
故选:D.
点评 本题考查直线与圆的位置关系,考查点到直线距离公式的运用,考查学生的计算能力,

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{9}$ |
| A. | sin2 | B. | -sin2 | C. | cos2 | D. | -cos2 |
| A. | f(1)<f(-3) | B. | f(3)>f(2) | C. | f(-2)>f(3) | D. | f(2)>f(0) |
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
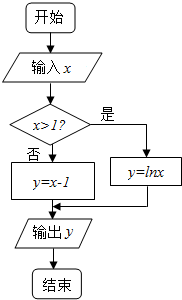 某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.
某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.