题目内容
9.已知数列{bn}满足bn=|$\frac{{a}_{n}+2}{{a}_{n}-1}$|,其中a1=2,an+1=$\frac{2}{{a}_{n}+1}$.(1)求b1,b2,b3,并猜想bn的表达式(不必写出证明过程);
(2)由(1)写出数列{bn}的前n项和Sn,并用数学归纳法证明.
分析 (1)由已知结合数列递推式求得b1,b2,b3,并猜想bn的表达式;
(2)由等比数列的前n项和公式求得数列{bn}的前n项和Sn,并用数学归纳法证明.
解答 解:(1)∵a1=2,an+1=$\frac{2}{{a}_{n}+1}$,∴${a}_{2}=\frac{2}{3}$,${a}_{3}=\frac{6}{5}$,
又bn=|$\frac{{a}_{n}+2}{{a}_{n}-1}$|,得b1=4,b2=8,b3=16,
猜想:${b}_{n}={2}^{n+1}$;
(2)由(1)可得,数列{bn}是以4为首项,2为公比的等比数列,
则有${S}_{n}=\frac{4×(1-{2}^{n})}{1-2}={2}^{n+2}-4$.
证明:当n=1时,${S}_{1}={2}^{1+2}-4=4$成立;
假设当n=k时,有${S}_{k}={2}^{k+2}-4$,
则当n=k+1时,${S}_{k+1}={S}_{k}+{b}_{k+1}={2}^{k+2}-4+{2}^{k+2}$=2k+3-4=2(k+1)+2-4.
综上,${S}_{n}={2}^{n+2}-4$成立.
点评 本题考查数列递推式,考查了等比数列的前n项和,训练了利用归纳法证明数列等式,是中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
20.已知函数f(x)=ex-ax有两个零点x1,x2,x1<x2,则下面说法正确的是( )
| A. | x1+x2<2 | B. | a<e | ||
| C. | x1x2>1 | D. | 有极小值点x0,且x1+x2<2x0 |
17.已知A,B是单位圆上的两点,O为圆心,且∠AOB=90°,MN是圆O的一条直径,点C在圆内,且满足$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$(λ∈R),则$\overrightarrow{CM}$•$\overrightarrow{CN}$的最小值为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -1 |
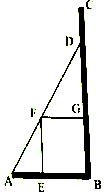 如图欲在直角区域ABC内的空地上植造一块“绿地Rt△ABD”,D在BC边上.其中AB=1,设BD=x(x>0)且BC足够长,规划在△ABD的内接正方形BEFG内种花,其余地方种草,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“完美度”.
如图欲在直角区域ABC内的空地上植造一块“绿地Rt△ABD”,D在BC边上.其中AB=1,设BD=x(x>0)且BC足够长,规划在△ABD的内接正方形BEFG内种花,其余地方种草,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“完美度”.