题目内容
已知函数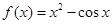 ,对于
,对于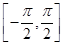 上的任意
上的任意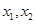 ,有如下条件:①
,有如下条件:①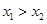 ;②
;②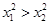 ;③
;③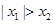 .其中能使
.其中能使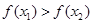 恒成立的条件序号是( )
恒成立的条件序号是( )
| A.①② | B.② | C.②③ | D.③ |
B
解析试题分析:显然函数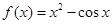 是
是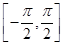 上的偶函数,且
上的偶函数,且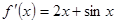 当
当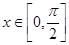 时
时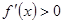 ,即函数
,即函数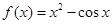 在
在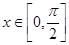 上单调递增,所以当
上单调递增,所以当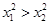 时则
时则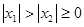 ,所以
,所以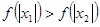 ,又
,又 是偶函数,所以
是偶函数,所以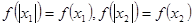 ,所以
,所以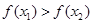 .
.
考点:奇偶性、导数分析单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 的零点所在的区间为( )
的零点所在的区间为( )
A. | B. | C. | D. |
给定函数①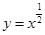 ,②
,②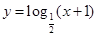 ,③
,③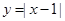 ,④
,④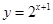 ,其中在区间(0,1)上单调递减的函数序号是( )
,其中在区间(0,1)上单调递减的函数序号是( )
| A.①② | B.②③ | C.③④ | D.①④ |
设 ,函数
,函数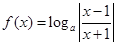 在
在 单调递减,则
单调递减,则 ( )
( )
A.在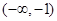 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在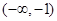 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在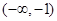 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在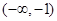 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
定义在R上的函数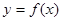 满足
满足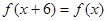 ,当
,当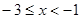 时,
时,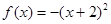 ,当
,当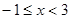 时,
时,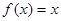 则
则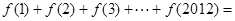 ( )
( )
| A.335 | B.338 | C.1678 | D.2012 |
 是R上以2为周期的奇函数,当
是R上以2为周期的奇函数,当 时
时 ,则
,则 在
在 时是( )
时是( )
A.减函数且 | B.减函数且 |
C.增函数且 | D.增函数且 |
关于 的不等式
的不等式 的解集非空的一个必要不充分条件是( )
的解集非空的一个必要不充分条件是( )
A. | B. | C. | D. |
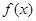 满足
满足 ,且在
,且在 [0,1]时,
[0,1]时,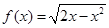 ,若直线kx-y+k=0(k>0)与函数
,若直线kx-y+k=0(k>0)与函数

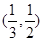

 的图象大致是( ).
的图象大致是( ).