题目内容
在△ABC中，若sinA=2sinBcosC，sin2A=sin2B+sin2C，则△ABC的形状是（ ）A．等边三角形
B．等腰三角形
C．直角三角形
D．等腰直角三角形
【答案】分析：通过正弦定理判断出三角形是直角三角形，通过sinA=2sinBcosC，利用正弦定理与余弦定理，推出三角形是等腰三角形，得到结果．
解答：解：因为sin2A=sin2B+sin2C，由正弦定理可知，a2=b2+c2，三角形是直角三角形．
又sinA=2sinBcosC，所以a=2b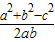
，解得b=c，三角形是等腰三角形，
所以三角形为等腰直角三角形．
故选D．
点评：本题考查三角形的形状的判断，正弦定理与余弦定理的应用，考查计算能力．
解答：解：因为sin2A=sin2B+sin2C，由正弦定理可知，a2=b2+c2，三角形是直角三角形．
又sinA=2sinBcosC，所以a=2b
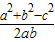，解得b=c，三角形是等腰三角形，所以三角形为等腰直角三角形．
故选D．
点评：本题考查三角形的形状的判断，正弦定理与余弦定理的应用，考查计算能力．
练习册系列答案
相关题目
在△ABC中，若sinA：sinB：sinC=5：7：8，则此三角形的最大角与最小角之和为（ ）
| A、90° | B、120° | C、135° | D、150° |