题目内容
设数列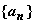 的前
的前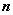 项和为
项和为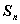 ,且
,且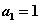 ,
,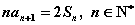 .
.
(Ⅰ)求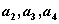 ;
;
(Ⅱ)求数列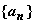 的通项公式;
的通项公式;
(Ⅲ)若数列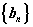 满足:
满足: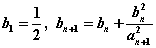 ,试证明:当
,试证明:当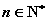 时,必有
时,必有
① ; ②
; ②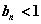
解:(Ⅰ)由 分别代入递推式即可得
分别代入递推式即可得 …………3分
…………3分
(Ⅱ)方法一:因 ,
,
两式相减得
即 ,即
,即
所以 ,
, ……7分
……7分
方法二:先猜想出 ,再用数学归纳法证明.
,再用数学归纳法证明.
(Ⅲ)①由(Ⅱ)得 ,所以
,所以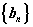 是正项
是正项
单调递增数列,当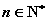 时,
时, 
所以 ,
, 即
即
②由①得,当 时,
时, ,
, ,…… ,
,…… ,
所以
即
所以


所以 , 即
, 即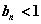

又当 ,
, . 故当
. 故当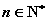 时,
时,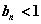

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目


 是定义在R上的可导函数,且当
是定义在R上的可导函数,且当 时,
时, ,则关于
,则关于 的函数
的函数 的零点个数为( )
的零点个数为( ) 的图像关于直线
的图像关于直线 对称,且图像上
对称,且图像上 和
和 的值; (Ⅱ)若
的值; (Ⅱ)若 ,求
,求 的值.
的值. 的公差为2,若
的公差为2,若 ,
, ,
, 成等比数列,则
成等比数列,则 的前n项和
的前n项和 ( )
( ) B、
B、 C、
C、
 D、
D、
 为等差数列,
为等差数列, ,
, ,则
,则 等于( )
等于( ) 与
与 互相垂直,垂足为
互相垂直,垂足为 ,则
,则 的值为
的值为 C.0 D.
C.0 D. 