Question

【题目】函数（满足：

（1），

（2）在区间内有最大值无最小值，

（3）在区间内有最小值无最大值，

（4）经过。

（1）求的解析式；

（2）若，求值;

（3）不等式的解集不为空集，求实数的范围.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

试题分析：（1）根据函数的对称性，可得函数的对称轴是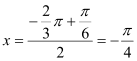，以及，再根据条件（2）（3）可得在处取得最大值，在处取得最小值，这样可知道函数的周期根据五点法求，根据条件（4）求A;（2）代入可求得，因为，这样，根据同角基本关系求解；（3）将问题转化为（其中），，即可解得的取值范围.

试题解析：（1）由条件（1）（2）（3）可知，和为相邻对称轴，且在处取得最大值，在处取得最小值.

所以得；由在处取得最大值得且。

经过，所以，解得

所以

（2）因为，所以；

（3）（其中）

，所以，解得：