题目内容
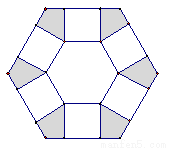
如图，边长为2的正六边形ABCDEF的中心在原点，点F、C在x轴上．
（1）求CD边所在的直线方程；
（2）若直线l与边CD相交，且平分该六边形的面积，求直线l的斜率的取值范围．
解：（1）由题意知C（2，0），D（1，
），用两点式写出CD边所在的直线方程 
=
，
即x+y-2=0．
（2）直线l过正六边形的中心，当直线l与边CD相交与点C时，直线l与x轴重合，斜率最小等于0，
当直线l与边CD相交与点D时，直线l即直线AD，方程即 y=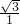
x，斜率最大等于，
故斜率的取值范围为[0，]．
分析：（1）求出C、D的坐标，用两点式写出CD边所在的直线方程，并化为一般式．
（2）直线l过正六边形的中心，当直线l与边CD相交与点C时，斜率最小；当直线l与边CD相交与点D时，斜率最大．
点评：本题考查用两点式求直线的方程的方法，斜率范围的确定方法，体现了数形结合的数学思想．
），用两点式写出CD边所在的直线方程 =，即
x+y-2=0．（2）直线l过正六边形的中心，当直线l与边CD相交与点C时，直线l与x轴重合，斜率最小等于0，
当直线l与边CD相交与点D时，直线l即直线AD，方程即 y=
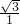x，斜率最大等于，故斜率的取值范围为[0，
]．分析：（1）求出C、D的坐标，用两点式写出CD边所在的直线方程，并化为一般式．
（2）直线l过正六边形的中心，当直线l与边CD相交与点C时，斜率最小；当直线l与边CD相交与点D时，斜率最大．
点评：本题考查用两点式求直线的方程的方法，斜率范围的确定方法，体现了数形结合的数学思想．
练习册系列答案
相关题目
如图，P-ABC是底面边长为1的正三棱锥，D、E、F分别为棱长PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF-ABC与棱锥P-ABC的棱长和相等．（棱长和是指多面体中所有棱的长度之和）
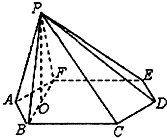（2012•武清区一模）如图，六棱锥P-ABCDEF的底面ABCDEF是边长为l的正六边形，顶点P在底面上的射影是BF的中点O．
PA, 求二面角D-BC-A的大小；(结果用反三角函数值表示)
